Коновалов В.А., доцент к.э.н., докторант ФГУП «СТАНДАРТИНФОРМ», Темиров К.В., доцент Северо-Осетинского государственного университета им. К.Л.Хетагурова

В рамках процессного подхода организации контроля и управления бизнес-процессами предприятия одной из важнейших задач является задача определения состояний бизнес-процессов.

 

Ключевые слова: бизнес процесс, производство, система.

 

ESTIMATION OF PROBABILITIES OF CONDITIONS OF BUSINESS PROCESSES OF THE ENTERPRISE

Konovalov V., the senior lecturer competitor FSUO «Standartinform», Temirov K., The senior lecturer of the North Ossetia state university of K.L.Hetagurova

Within the limits of the process approach of the organization of the control and management of business processes of the enterprise of one of the major problems the problem of definition of conditions of business processes is.

 

Key word: business process, production, system.

 

Уточним понятие «состояние бизнес-процесса». В соответствии с определением¹ бизнес-процесс – это совокупность целенаправленных созидательных действий по производству и поставке продукции для внутренних и внешних потребителей.

Любое целенаправленное созидательное действие по производству и поставке продукции для внутренних и внешних потребителей с позиции системного подхода² может рассматриваться как элемент, а их совокупность как система.

Элемент – неделимая часть, лежащая в основе построения системы. Неделимость элемента рассматривается как нецелесообразность учета в пределах системы его внутреннего строения. Сам элемент характеризуется только его внешними проявлениями в ходе отношений и взаимодействий с остальными элементами и окружающей средой. Элемент с течением времени может изменяться, переходить в различные состояния.

Состояние элемента – это пространственная упорядоченная субстанция элемента в определенный момент времени, проявляющаяся в его отношениях и взаимодействиях с окружающей средой. Можно сказать, что состояние – это элемент в определенный момент времени.

Состояние элемента можно определять с помощью набора величин, характеризующих его свойства, пространственное расположение и внешние проявления в данном состоянии. Иногда, хотя это не совсем точно, состояние определяют как набор этих величин (параметров). В общем случае из-за неисчерпаемости субстанции любого материального элемента число таких величин может быть очень велико, поэтому целесообразно ограничиться некоторым набором из них, характеризующим наиболее существенное влияние элемента на систему.

Состояние системы – совокупность состояний ее элементов, отношений, связей и взаимодействий между ними и окружающей средой в определенный момент времени.

Состояние системы, по аналогии состоянию элемента, можно определить с помощью набора величин (параметров), характеризующих свойства, пространственное расположение и внешние проявления системы. Поэтому в ряде случаев, хотя не совсем точно, под состоянием системы понимают упорядоченную совокупность значений параметров, определяющих «поведение» системы или наиболее полно характеризующих систему. Можно сказать, что состояние системы – это система в определенный момент времени.

Тогда состояние бизнес-процесса – это упорядоченная совокупность значений параметров, определяющих динамику бизнес-процесса или наиболее полно характеризующих его.

Контроль состояния бизнес-процессов предприятия позволит отслеживать их состояние, оценивать уровень задействования занятых в них человеческих, материальных, финансовых и информационных ресурсов, определять ключевые показатели бизнес-процессов и их соответствие требуемым показателям. По результатам контроля бизнес-процессов и анализа их состояния могут быть приняты обоснованные решения об управлении бизнес-процессами:

-         оставить бизнес-процессы без изменения;

-         принять меры «локального» характера, не требующие полной перестройки или проведения оптимизации бизнес-процессов, т.е. меры, требующие настройки (регулировки) или совершенствования бизнес-процессов в соответствии с установленными для них регламентами (стандартами предприятия)³;

-         принять меры «глобального» характера, требующие полной перестройки или проведения оптимизации бизнес-процессов. Бизнес-процессы, требующие полной перестройки или проведения оптимизации, в экономической литературе называют проблемными, критическими, аномальными⁴, хотя более правильно вести речь об определенном состоянии соответствующего бизнес-процесса.

При выпуске определенной продукции в рамках функционирующего предприятия, как правило, имеют место решения первого и второго типа, в случае решений третьего типа изменяется и само предприятие и выпускаемая им продукция, поэтому далее рассматриваем только решения первых двух типов.

Решение задачи контроля и управления бизнес-процессами предприятия предполагает наличие их экономико-математической модели. В наиболее общем виде модель любого объекта может быть представлена упорядоченным множеством

� = < T, X, Y, Z, F, G > , (1)

где T – множество моментов времени t, в которые наблюдается объект;

X, Y – множества входных и выходных сигналов соответственно;

Z – множество состояний объекта;

F – оператор переходов, отражающий механизм изменения объекта под воздействием внутренних и внешних возмущений;

G – оператор выходов, описывающий механизм формирования выходного сигнала как реакции объекта на внутренние и внешние возмущения.

Операторы F и G реализуют отображения

F: T x X x Z � Z; (2)

G: T x X x Z � Y. (3)

Всякое состояние объекта Z характеризуется в каждый момент времени t набором переменных, изменяющихся под воздействием внутренних и внешних возмущений. Состояние объекта есть набор таких переменных, которые хотя и полностью определяют положение объекта как некоторой абстрактной динамической системы в некотором пространстве в рассматриваемый момент времени, но сами по себе не позволяют установить правильно ли функционирует объект. Для того чтобы вынести такое суждение, необходимо сопоставить каждую переменную состояния объекта с некоторым конкретным значением, характеризующим уровень эффективности функционирования. Только на основании результатов сопоставления всех

переменных состояния объекта с априорно заданными их значениями можно отнести состояние объекта к тому или иному виду состояний. Однако такое сопоставление не всегда осуществимо, т.к. переменные состояния z_i в общем случае являются некоторыми абстрактными переменными и их непосредственный контроль не всегда возможен.

В отличие от них выходные переменные y_i всегда можно наблюдать и контролировать. В этом отношении выходные параметры являются более удобными для использования их в качестве признаков при определении состояния объекта. Иными словами, определение состояния любого объекта практически осуществляется не в пространстве переменных состояния, а в пространстве выходных параметров.

С математической точки зрения определение любого состояния объекта возможно только в том случае, если по результатам измерения выходных параметров y_i (i=1,2,…,l) при известных значениях входных переменных

x_k (k = 1,2,…, m) может быть получена оценка любой из переменных состояния объекта z_j (j = 1,2,…,n). Такая задача в теории систем и управления известна как задача наблюдения. Она состоит в том, чтобы на основе известного выходного процесса определить неизвестные состояния объекта.

Необходимым и достаточным условием полной наблюдаемости объекта является инъективность отображения (3), при которой каждый

элемент в случае фиксированных  и Х(t) имеет в качестве прообраза единственный элемент . Это означает, что всякому изменению вектора выхода Y(t) при фиксированном векторе X(t) соответствует определенное изменение вектора состояния объекта.

При полной наблюдаемости объекта всегда возможно определение его состояния по данным контроля. Но конечной целью контроля является определение одного из заданных видов (классов) состояний. Задача отнесения наблюдаемого состояния объекта к одному из заданных видов его состояний называется задачей классификации. Решение этой задачи заключается в отыскании отображения

ψ :Y → E , (4)

где Е – множество видов состояний объекта.

Каждому виду состояний объекта соответствует определенное подмножество его текущих состояний, объединенных некоторыми общими свойствами, т.е. таких состояний, о которых может быть принято одно и то же решение. Отдельные состояния, входящие в это подмножество, должны находиться в отношении эквивалентности. Напомним, что отношением эквивалентности называется бинарное отношение Q = Y x Y, обладающее свойствами рефлексивности, симметричности и транзитивности⁵.

Отношение эквивалентности задает разбиение множества Y всех состояний объекта на непересекающиеся подмножества или классы, т.е. осуществляет факторизацию этого множества.

В ряде случаев разбиение исходного множества Y на непересекающиеся подмножества выполняется естественным образом, например, исходное множество делится на два подмножества, в одном из которых некоторое условие выполняется, а в другом подмножестве – не выполняется.

Аналогично все множество состояний бизнес-процесса разделим на два подмножества: подмножество состояний А, соответствующее нормальному исполнению бизнес-процесса или соответствующее его регламенту, при котором выпускается продукция необходимого качества и подмножество состояний В, несоответствующее нормальному исполнению бизнес-процесса или несоответствующее его регламенту, при котором не выпускается продукция необходимого качества. Тогда условием выпуска качественной продукции будет соответствие состояний всех бизнес-процессов своим регламентам или – чтобы все бизнес-процессы находились в подмножестве состояний А, соответствующем нормальному исполнению бизнес-процессов.

Любое состояние бизнес-процесса есть случайное событие, зависящее от большого числа факторов, с течением времени, как правило, любой бизнес-процесс переходит из состояния А в состояние В, несоответствующее нормальному исполнению бизнес-процесса или несоответствующее регламенту бизнес-процесса, при котором не выпускается продукция необходимого качества.

Предположим, что для выпуска основной продукции предприятия должны быть задействованы и исполнены n бизнес-процессов (n >0). Каждый j-ый бизнес-процесс в произвольный момент времени может находиться в состоянии А_j или состоянии B_j. Пусть вероятность перехода j-го бизнес-процесса в состояние В_j равна q_j, р_j= 1-q_j (j=1,2,…,n), причем переходы всех бизнес-процессов из состояния А_j в состояние B_j взаимнонезависимы. Считаем, что одновременно может только один бизнес-процесс перейти из состояния Аj в состояние B j, хотя в принципе могут перейти из состояния А_j в состояние B_j два и более бизнес-процесса, но вероятность таких событий ничтожно мала и поэтому ее не рассматриваем.

Определим гипотезу μ_j как гипотезу, состоящую в том, что j-ый бизнес-процесс перешел из состояния А_j  или состоянии B_j , j = 1,2,…,n. Гипотеза μ₀ заключается в том, что все n бизнес-процессов находятся в состоянии А_j.

Поставим в соответствие гипотезе μ_i состояние бизнес-процессов предприятия е_i i = 0,1,…,n.

Задача состоит в том, чтобы определить вероятность нахождения бизнес-процессов в любом из рассматриваемых состояний е_i i = 0,1,…,n или вероятность i-го состояния бизнес-процессов предприятия Р(е_i).

Вероятности гипотез Р(μ_i) определяются через значения вероятностей q_j (j=1,2,...,n) перехода j-го бизнес-процесса в состояние В_j по следующим формулам⁶:

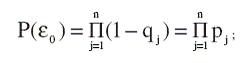 (5)

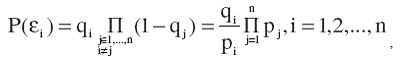 (6)

 где p_j = 1-q_j – вероятность нахождения j-го бизнес-процесса в состоянии А. Рассмотренные гипотезы μ₀, μ₁,…,μ_n не составляют полную группу событий, так как не охватывают ряд возможных ситуаций, обусловленных переходом из состояния А в состояние В нескольких бизнес-процессов одновременно. Поэтому

Вероятности Р(μ₀), Р(μ₁), …, Р(μ_n) есть априорные (доопытные) вероятности выдвинутых гипотез. Опыт заключается в проверке выполнимости заданных условий. Эти условия заключаются в том, что бизнес-процессы предприятия могут находится в состоянии А – состояние е₀, либо хотя бы один бизнес-процесс перейдет в состояние В; обозначим это состояние е_B; при этом конкретный бизнес-процесс, перешедший в состояние В не важен, а важен факт перехода одного из бизнес-процессов в состояние В. Наблюдаемым исходом опыта (наблюдения) будет событие е₀ U е_B. Тогда апостериорные (послеопытные, уточненные) значения вероятностей гипотез определяются по формуле Байеса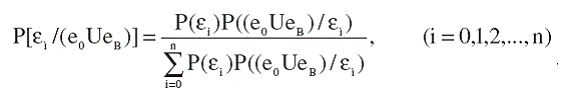⁷:

 (7)

Апостериорные значения вероятностей гипотез дают искомые вероятности соответствующих состояний нахождения бизнес-процессов или вероятность i-го состояния бизнес-процессов предприятия Р(е_i)

 (8)

В формуле (7) условные вероятности равны единице, т.е.

, (9)

если бизнес-процессы находятся в одном из возможных состояний μ_i , то это состояние либо e₀, либо e_B . Выполнив соответствующие преобразования, найдем вероятность состояний е₀ и е_i

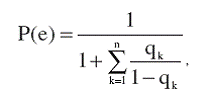 (10)

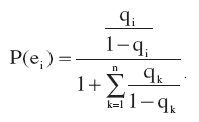 (11)

Так как в соответствии с выражением (9) полученные вероятности есть значения вероятностей соответствующих гипотез μ_i (i = 0,1,2,..., n.), уточненных по результатам опыта, в котором подтвердились заданные условия, то рассматриваемые состояния бизнес-процессов е_i можно считать событиями, составляющими полную группу, поэтому должно выполняться равенство

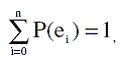
которое, как следует из формул (10) и (11), выполняется.

Далее определим вероятности состояний бизнес-процессов. В данном случае считается достоверно установленным, что бизнес-процессы находятся в состоянии е_B, и требуется установить, какой из бизнес-процессов перешел в состояние В. Соответственно этому выдвинем в качестве рабочих гипотез гипотезы μ_i, каждая из которых предполагает переход из состояния А в состояние В i-го процесса. Априорные значения вероятностей гипотез определятся в соответствии с соотношением (6):

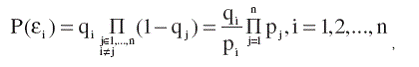
а их апостериорные значения по формуле Байеса:

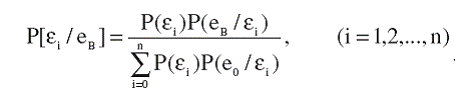 (12)

Так же как и в предыдущем случае полагаем очевидным равенства

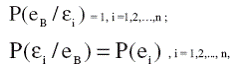
с учетом которых из соотношения (12) получаем

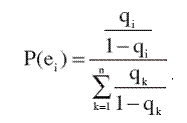 (13)

Из формулы (13) непосредственно следует, что

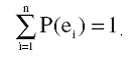
Далее рассмотрим случай, когда при выпуске продукции задействованы различные бизнес-процессы из их общего числа. Каждую задействованную комбинацию бизнес-процессов при выпуске продукции назовем бизнес-режимом. При выпуске продукции бизнес-режимы последовательно сменяют друг друга. Пусть общее число таких режимов m. Требуется определить вероятность перехода бизнес-процессов в каждый бизнес-режим, рассматривая самостоятельные состояния бизнес-процессов предприятия.

В каждом бизнес-режиме могут участвовать разные бизнес-процессы. Обозначим N_i подмножество бизнес-процессов, задействованных в i-ом бизнес-режиме i = 1,2,…,m. Тогда априорная вероятность гипотезы μ_i о нахождении бизнес-процессов в i-ом бизнес-режиме определится по формуле

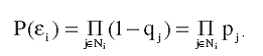 (14)

Формула Байеса для определения апостериорных значений вероятностей гипотез μ_i примет вид

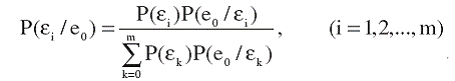 (15)

При этом Р(е₀/μ_i) = Р(е_i/μ_k) = 1 для всех i,k = 1,2,…,m, так как в процессе нормального исполнения бизнес-процессов исполняется нормально один из бизнес-режимов предприятия. Подставляя в формулу (15) равенство (14) и учитывая, что

 

получаем

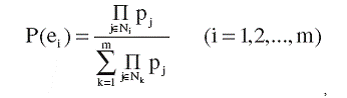 (16)

где N_k – подмножество бизнес-процессов, участвующих в формировании k – бизнес-режима функционирования предприятия. Можно проверить из формулы (16), что

 

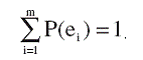
При контроле состояния бизнес-процессов наряду с контролем их переходов из одного состояния нормальной работы в другой, очень важным является установление факта перехода бизнес процессов из состояния А в состояние В. Наряду с выдвинутыми гипотезами μ_i (i = 1,2,…,m), введем гипотезу μ_И , соответствующую переходу из состояния А в состояние В хотя бы одного из бизнес-процессов в любом бизнес-режиме. Априорная вероятность этой гипотезы равна

 

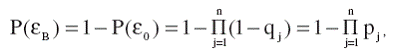
с учетом которой по формуле Байеса получим

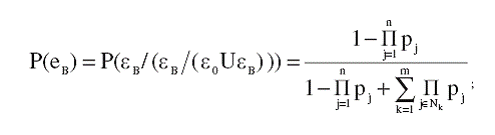 (17)

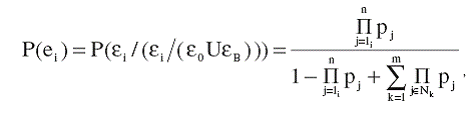 (18)

Правильность последних соотношений устанавливается проверкой условия

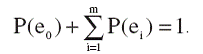 (19)

Таким образом, в настоящей работе определены основные соотношения для определения вероятностей состояний бизнес-процессов предприятия.

 

1 Темиров К.В., Коновалов В.А. Модели оптимальной реализации организационно-управленческих резервов повышения качества продукции. - М.: Стандартинформ, 2007.

2 См.: Ерохина Е.А. Теория экономического развития: системно-синергетический подход. М., 1999; Миротин Л.Б., Ташбаев Ы.Э. Системный анализ в логистике. М.: Экзамен. 2002.

3 Стандарт на процесс (то, как надо выполнять работу). Пример: регламент бизнес-процесса – документ, содержащий подробное описание какого-либо процесса компании, включая схему выполнения работ. Если вы стандартизируете процесс – то исключаете максимум возможных ошибок и тем самым способствуете повышению качества результата процесса.

4 См.: Харрингтон Д., Эсселинг К., Нимверген Х. Оптимизация бизнес-процессов: документирование, анализ, управление, оптимизация. СПб: «Азбука», 2002; Волчков С.А., Балахонова И.В. Непрерывное улучшение бизнес-процессов на базе стандартов ERP и ИСО серии 9000 // Методы менеджмента качества. 2001. №2.

5 См.: Калинин В.Н., Резников Б.А., Варакин Е.Н. Теория систем и оптимального управления. Л.: ВИКА, 1979.

6 См.: Математические методы в теории систем / Под ред. Ю.И.Журавлева. М.: Мир, 1979.

7 См.: Пугачев В.С. Теория вероятностей и математическая статистика. М.: Физматлит, 2002.

 

Литература:

1.        Волчков С.А., Балахонова И.В. Непрерывное улучшение бизнес-процессов на базе стандартов ERP и ИСО серии 9000 // Методы менеджмента качества. 2001. №2.

2.        Ерохина Е.А. Теория экономического развития: системно-синергетический подход. М., 1999.

3.        Калинин В.Н., Резников Б.А., Варакин Е.Н. Теория систем и оптимального управления. Л.: ВИКА, 1979.

4.        Математические методы в теории систем / Под ред. Ю.И.Журавлева. М.: Мир, 1979.

5.        Миротин Л.Б., Ташбаев Ы.Э. Системный анализ в логистике. М.: Экзамен. 2002.

6.        Пугачев В.С. Теория вероятностей и математическая статистика. М.: Физматлит, 2002.

7.        Темиров К.В., Коновалов В.А. Модели оптимальной реализации организационно-управленческих резервов повышения качества продукции. - М.: Стандартинформ, 2007.

8.        Харрингтон Д., Эсселинг К., Нимверген Х. Оптимизация бизнес-процессов: документирование, анализ, управление, оптимизация. СПб: «Азбука», 2002.