Божкова Л.В., д.т.н., профессор, Рябов В.Г., к.т.н., профессор, Норицина Г.И., к.т.н., доцент

Московский государственный технический Университет «МАМИ»

Из опыта управления автомобилем известно, что при объезде препятствия с большой скоростью на горизонтальном участке дороги может произойти опрокидывание автомобиля без предварительного заноса.

В данной работе построена математическая модель динамики опрокидывания автомобиля при объезде препятствия. При этом по сравнению с имеющимися работами по этой тематике учтены поперечные вынужденные колебания кузова автомобиля.

В результате получена принципиальная возможность определения оптимальных соотношений конструктивных и эксплуатационных параметров различных типов автомобиля, обеспечивающих устойчивость его движения при объезде препятствия.

 

Ключевые слова: поперечные колебания, опрокидывание, управление автомобилем, объезд препятствий.

 

INFLUENCE OF THE CROSS-SECTION FORCED FLUCTUATIONS OF A BODY ON CAR OVERTURNING AT AN OBSTACLE DETOUR

Bozhkova L., professor, Ryabov V., professor, Noritsina G., senior lecturer

MSTU «MAMI» Influence of the cross-section forced fluctuations of a body on car overturning at an obstacle detour

From driving experience it is known that at a detour of an obstacle to a great speed on a horizontal part of the road there can be an overturning of the car without preliminary drift.

In the given work the mathematical model of dynamics of overturning of the car is constructed at an obstacle detour. Thus in comparison with present works on these subjects the cross-section forced fluctuations of a body of the car are considered.

Basic possibility of definition of optimum parities of constructive and operational parametres of various types of the car ensuring stability of its movement at a detour of an obstacle is as a result received.

 

Key words: cross-section fluctuations, overturning, driving, detour of obstacles.

 

Из опыта управления автомобилем известно, что при объезде препятствия с большой скоростью на горизонтальном участке дороги может произойти опрокидывание автомобиля без предварительного заноса.

В теории автомобиля считают, что при движении автомобиля по кривой траектории горизонтальной дороги, поперечной силой, которая может вызвать опрокидывание автомобиля, является только центробежная сила инерции. Однако, как показывают экспериментальные исследования /1/, найденные в этом случае значения критической скорости, при которой должно произойти опрокидывание, являются существенно завышенным, то есть опрокидывание может происходить при значительно меньших скоростях.

В /1/ приведено уточнение значений критической скорости автомобиля путем учёта поперечного крена кузова автомобиля, обусловленного наличием упругих элементов (пружин, рессор). При этом рассмотрен случай равномерного движения автомобиля по горизонтальной дороге с закруглением постоянного радиуса. Это позволило угол крена кузова найти на основании уравнений статики, то есть найти статическое отклонение кузова от вертикали.

Однако при объезде препятствия траектория автомобиля всегда имеет переменный радиус кривизны. Следовательно, центробежная сила инерции не будет постоянной и кузов автомобиля будет совершать вынужденные поперечные колебания.

Возмущающей силой является при этом центробежная сила инерции.

В /2/ приведена желаемая (с позиций водителя) траектория движения автомобиля при объезде препятствия (рис.1).

 

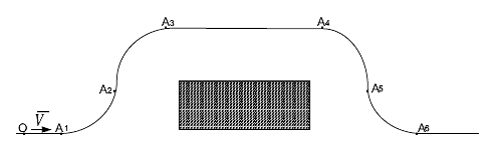
Рис.1. Траектория движения автомобиля при объезде препятствия.

 

При этом предполагается, что на участке дороги А₁ А₂ радиус кривизны плавно уменьшается от Ґ до некоторого конечного значения r, а на участке А₂ А₃ радиус кривизны также плавно растет от r до Ґ и т.д. Как утверждается в /2/, в данном случае (при плавном изменении радиуса кривизны траектории автомобиля, а значит и центробежной силы инерции) угол крена кузова автомобиля при поперечных колебаниях может увеличиваться в 1,3-1,5 раза по сравнению со статическим значением этого угла.

Однако, действительная траектория движения автомобиля при объезде препятствий может существенно отличаться от желаемой. Это особенно относится к тем случаям, когда препятствие на пути движения автомобиля возникает внезапно. При этом радиус кривизны в точке траектории А₁ может измениться скачком от Ґ до r. Следовательно, в этой точке может внезапно возникнуть центробежная сила инерции. В свою очередь в точке А₂, которая является точкой перегиба траектории движения автомобиля, уже имеющаяся сила инерции прекращает своё действие, но при этом так же внезапно возникает центробежная сила инерции противоположного направления. В точке А₃ внезапно прекращает свое действие центробежная сила инерции, возникающая на участке траектории А₂А₃, и т.д.

Из опыта вождения автомобилем известно, что указанный выше режим объезда препятствия является самым опасным с точки зрения опрокидывания автомобиля. В связи с этим целесообразно исследовать поперечные колебания автомобиля, обусловленные внезапно возникающими центробежными силами инерции, и оценить влияние этих колебаний на опрокидывание автомобиля.

Принято считать, что опрокидывание автомобиля может начаться в тот момент, когда реакции дорожного полотна на правые или левые колеса автомобиля равны нулю. В связи с этим сначала определим реакции дорожного полотна на колеса автомобиля в зависимости от выше перечисленных динамических факторов.

Прежде всего рассмотрим случай равномерного движения автомобиля (со скоростью V) как единого твердого тела на участке криволинейной траектории А1 А 2 . Для определенности участки криволинейной траектории А₁А₂ , А₂А₃ , А₄А₅, А₅А₆ далее будем считать дугами окружностей одного и того же радиуса r.

При равномерном движении автомобиля на участке криволинейной траектории А₁А₂ (дуги окружности) возникает центробежная сила инерции, величина которой зависит от массы автомобиля, его скорости и радиуса дуги окружности /3/:

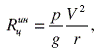 (1)

где р - вес автомобиля, V – его скорость, g – ускорение свободного падения, r – радиус дуги окружности А₁А₂.

Для определения результирующих реакций дорожного полотна N1 и и N2 и , действующих соответственно на левые и правые колеса автомобиля, применим принцип Даламбера /3/ (рис.2).

 

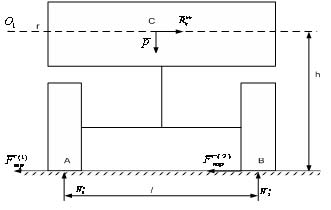
Рис.2. Расчетная схема сил, действующих на автомобиль (как единое твердое тело) при его движении по дуге окружности А₁А₂

 

Приведенная на рисунке 2 расчетная схема сил соответствует случаю, когда центр масс автомобиля находится на средине между осями передних и задних колес. Данное допущение не может привести к заметному изменению величины искомых реакций.

Таким образом, для определения реакций  и и составим на основании расчетной силовой схемы (рис.2) два уравнения кинетостатики: приравняем к нулю суммы моментов всех сил относительно точек А и В. В результате с учетом (1) и принятого допущения о симметрии передней и задней осей колес по отношению к центру масс автомобиля нетрудно найти реакции дорожного полотна, действующие в отдельности соответственно на каждое колесо.

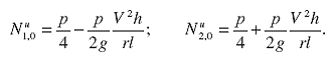 (2)

Начало опрокидывания автомобиля возможно при  (3)

На основании (2) с учетом (3) нетрудно найти критическую скорость автомобиля, при которой возможно его опрокидывание.

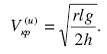 (4)

Как было указано ранее, значение критической скорости, найденной на основании (4), является завышенным.

Поэтому далее оценим влияние поперечных колебаний подрессоренных масс (кузова) автомобиля, вызванные внезапным возникновением центробежной силы инерции, на его опрокидывание при объезде препятствия.

Будем считать, что центробежная сила инерции автомобиля в точке траектории А₁ () (рис.1) возникает внезапно, а в точке А₂ эта сила прекращает свое действие и внезапно возникает центробежная сила инерции

противоположного направления. В свою очередь, в точке А3 центробежная сила инерции также внезапно прекращает свое действие и т.д. Для определенности полагаем, что участки траектории А₁А₂ и А₂А₃ представляют собой дуги окружностей радиуса r, равные четверти длины окружности, а именно:

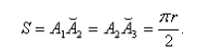(5)

Кроме того, скорость движения автомобиля V на протяжении всего времени объезда препятствия считаем постоянной. Внезапно возникающие центробежные силы инерции будут действовать в течение некоторого промежутка времени t, определяемого по формуле

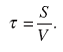 (6)

Учитывая отношение (5), на основании (6) получим

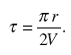 (7)

Таким образом, характер изменения центробежной силы инерции автомобиля при объезде препятствия описывается, так называемой, ступенчатой функцией (рис.3).

 

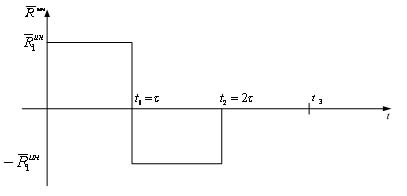
Рис.3. Характер изменения центробежной силы инерции на участке траектории А₁, А₂ , А₃

 

Величины центробежных сил инерции  определяются по формуле (1). Центробежные силы инерции (возмущающие силы) вы

зовут относительные поперечные колебания кузова автомобиля вокруг оси крена.

Рассмотрим в первом приближении плоскую колебательную систему, аналогичную расчетной схеме представленной на рис.2. Для определенности считаем, что центр крена плоского сечения (т.С_v) расположен на оси колес (рис.4), а жесткости эквивалентных пружин с э определяются по формуле

 (8)

где с_р - коэффициенты жесткости всех пружин.

 

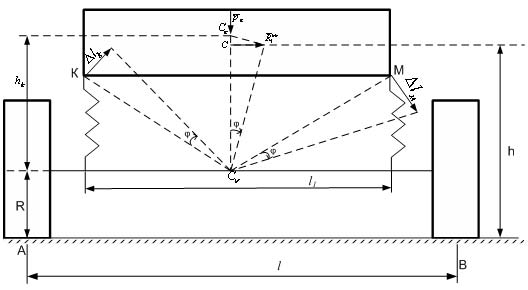
Рис.4. Расчетная схема поперечных колебаний кузова

 

На рис.4 введены следующие обозначения: R – радиус колес; Р_к– сила тяжести кузова; С_к – центр масс кузова; Δl_К и Δl_М перемещение точек крепления пружин к кузову в результате его поворота вокруг центра крена (т.С_v) на угол j. Рассмотренная механическая система имеет одну степень свободы. За обобщенную координату системы примем угол j отклонения кузова от вертикали (рис.4). Система находится под действием потенциальных сил – силы тяжести кузова, сил упругости двух эквивалентных пружин, а также под действием возмущающей силы, равной центробежной силе инерции автомобиля. Силой сопротивления на первом этапе пренебрегаем.

Уравнение Лагранжа второго рода в данном случае имеет вид:

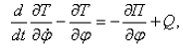(9)

где: Т – кинетическая энергия системы; П – потенциальная энергия; Q - обобщенная возмущающая сила, обусловленная действием центробежной силы инерции. Кинетическую энергию системы (подрессорных масс автомобиля) приближенно можно представить в виде:

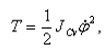 (10)

где J_Cv - момент инерции кузова относительно продольной оси, проходящей через точку С_v.

Потенциальная энергия системы складывается из потенциальной энергии силы тяжести кузова автомобиля и потенциальной энергии двух эквивалентных пружин.

Ограничиваясь величинами второго порядка малости, выражение потенциальной энергии системы можно представить в виде:

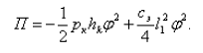 (11)

Определим обобщенную силу Q , соответствующую возмущающей силе (центробежной силе инерции ). С этой целью найдем элементарную работу силы  на элементарном перемещении системы, соответствующем приращению обобщенной координаты δϕ :

 (12)

Как следует из рисунка 4  (13)

В результате подстановки (13) и (1) в (12) получим:

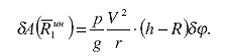 (14)

Обобщенная сила Q, соответствующая обобщенной координате j, определяется по формуле

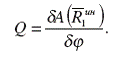 (15)

На основании (15) с учетом (14) найдем

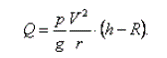 (16)

В результате подстановки (10), (11) и (16) в уравнение (9) получим:

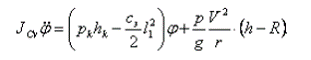 (17)

Учитывая (8), преобразуем дифференциальное уравнение (17) к виду:

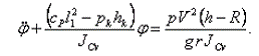 (18)

На основании теоремы Лагранжа – Дирихле /3/ нетрудно убедиться в том, что вертикальное положение кузова будет положением устойчивого равновесия в случае выполнения неравенства

. (19)

Таким образом, согласно (19) коэффициент при переменной j в уравнении (18) является положительным. Введем в связи с этим следующие обозначения:

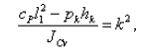 (20)

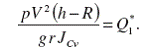(21)

В результате с учетом обозначений (20) и (21) дифференциальное уравнение (18) примет вид:

 (22)

Найдем решение дифференциального уравнения (22) при нулевых начальных условия в случае, когда обобщенная возмущающая сила Q* в соответствии с характером изменения центробежной силы инерции (рис.3) описывается также ступенчатой функцией (рис.5).

 

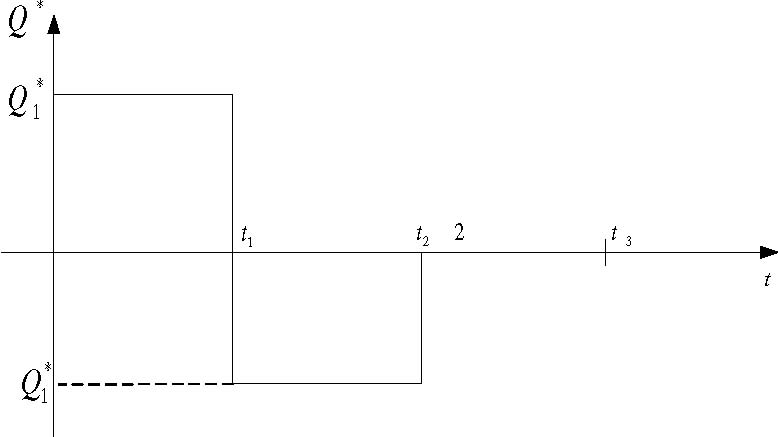
Рис.5. Характер изменения обобщенной возмущающей силы на участке траектории А₁А₂А₃.

 

При этом решение дифференциального уравнения (22) будет иметь вид /4/:

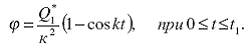 (23)

Колебания, определяемые уравнением (23), существуют до тех пор, пока действует сила Q₁^* , то есть при t ≤τ (при движении автомобиля на участке траектории А₁А₂).

Чтобы определить закон поперечных колебаний кузова на следующем участке траектории (А₂А₃), можно применить принцип суперпозиции действия сил. На участке траектории А 2 А 3 действует возмущающая сила − Q₁^*. Суть метода суперпозиции заключается в следующем. Считаем, что возмущающая сила Q₁^* действует в течение всего времени t ≥ 0 , а в момент времени t = t₁ внезапно возникает возмущающая сила, равная −2Q₁^* (рис.6).

Под действием возмущающей силы −2 Q₁^* в момент времени t = t₁ возникнут колебания. Уравнения этих колебаний можно представить в виде уравнения аналогичного (23), то есть

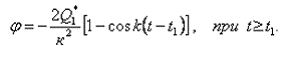 (24)

 

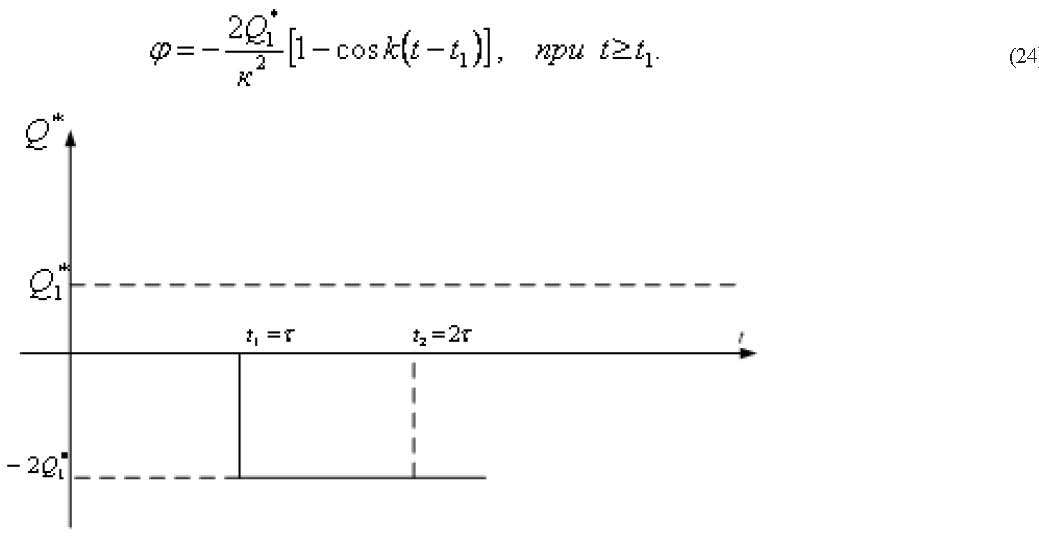
Рис.6. Расчетная схема изменения обобщенных возмущающих сил при применении принципа суперпозиции.

 

На основании принципа суперпозиции уравнение колебания кузова автомобиля на участке траектории А₂А₃ (т.е. при t ≥t₁ ) определится как сумма (23) и (24):

 (25)

Следует обратить внимание на тот факт что колебания, определяемые уравнением (25), существуют в течение действия силы − Q^* (рис.5). После очевидного преобразования получим:

 (26)

Возмущающая сила − Q^* в момент времени t = t₂ внезапно прекращает свое действие. Уравнение колебаний кузова, при t ≥ t₂ можно найти аналогично (26), применяя принцип суперпозиции. В результате получим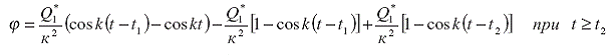

После очевидных преобразований данное уравнение примет вид:

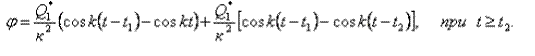 (27)

Аналогично можно найти при необходимости уравнения поперечных колебаний кузова на участках его траектории А₄А₅ и А₅ А₆.

Прежде всего, исследуем уравнение (23) поперечных колебаний кузова при движении автомобиля на первом участке траектории А₁А₂. С этой целью определим ближайший момент времени t, при котором угол отклонения кузова от вертикали будет максимальным.

Приравнивая обобщенную скорость φ нулю, получим

Отсюда следует, что при

 (28)

функция (23) имеет максимум или минимум. Так как вторая производная по времени от обобщенной координаты при t = t_* меньше нуля, то в этот момент времени угол j достигает максимального значения. На основании (23) с учетом (28) определяем

 (29)

Период собственных колебаний системы определяется по формуле

 (30)

Из сравнения (28) и (30) следует, что угол отклонения кузова от вертикали при движении автомобиля на участке траектории А₁А₂ достигает максимального значения в том случае, когда промежуток времени равен t_* половине периода собственных колебаний кузова.

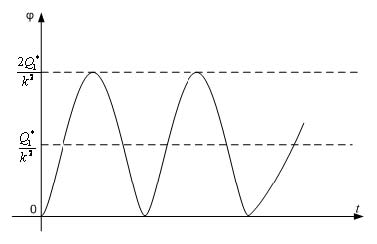
Рис. 7. График поперечных колебаний кузова автомобиля на участке траектории А₁А₂

 

Нетрудно убедиться, что угол статического отклонения кузова от вертикали определится по формуле

 (31)

Следовательно, из приведенного решения (23) следует, что при внезапном приложении в точке А₁ траектории автомобиля постоянной

центробежной силы инерции, возникают поперечные колебания кузова с амплитудой , наложенные на статическое отклонение той же величины (31) (рис.7). Таким образом, максимальный угол отклонения кузова автомобиля от вертикального положения при внезапном приложении центробежной силы инерции в два раза больше угла ϕ_ст, обусловленного статическим приложением этой силы.

Если время движения автомобиля на участке траектории А₁А₂ , то угол наклона кузова достигнет своего максимального значения после внезапного прекращения действия центробежной силы инерции  и внезапного возникновения центробежной силы инерции  (рис.3), то есть при движении на участке траектории А₂А₃. Момент времени t_М ≥ τ , когда угол наклона кузова автомобиля при его движении на участке траектории А₂А₃ достигнет максимума, можно определить на основании уравнения движения (26).

Приравнивая обобщенную скорость φ нулю, получим:

 (32)

Из (32) следует, что при

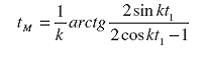 (33)

функция (26) имеет максимум. На основании (26) с учетом (33) определяем

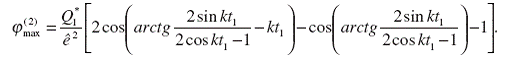 (34)

Нетрудно убедиться, что в случае, когда время движения автомобиля на участке траектории А₁А₂

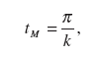 (35)

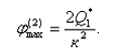 (36)

Таким образом, наибольший угол наклона кузова автомобиля при его движении на участке траектории А₁А₂А₃ будет в точке перегиба траектории (т.е. в т. А₂) при условии, что время движения на участке А₁А₂ равно половине периода поперечных колебаний кузова. Далее определим влияния поперечных колебаний автомобиля на его опрокидывание. С этой целью необходимо определить реакции дорожного полотна на колеса автомобиля в случае, когда угол наклона кузова будет максимальным.

Для определения результирующих реакций дорожного полотна  и , действующих соответственно на левые и правые колеса

автомобиля в момент максимального наклона кузова, применим принцип Даламбера /3/. С этой целью присоединим к силам, действующим на автомобиль (сила тяжести автомобиля и реакции дорожного полотна), центробежную силу инерции автомобиля, а также главный вектор и главный момент сил инерции кузова при его поперечных колебаниях. Модули касательной и нормальной составляющей главного вектора сил инерции кузова определяются соответственно по формулам:

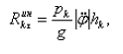 (37)

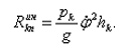 (38)

Модуль главного момента сил инерции кузова равен

 (39)

где  - момент инерции кузова относительно продольной оси, проходящей через центр масс кузова.

При этом и  направлены противоположно угловому ускорению (направление углового ускорения определяется знаком

На основании (26) найдем:

 (40)

Определим и  в момент, когда угол наклона кузова будет максимальным, то есть в момент 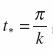 при условии, что при этом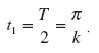

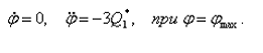 (41)

На основании (37) – (39) и (41) получим

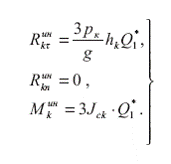 (42)

Для определения реакции  и  на основании расчетной силовой схемы (рис.8) составим два уравнения кинетостатики: приравниваем к нулю суммы моментов всех сил относительно точек А и В.

 

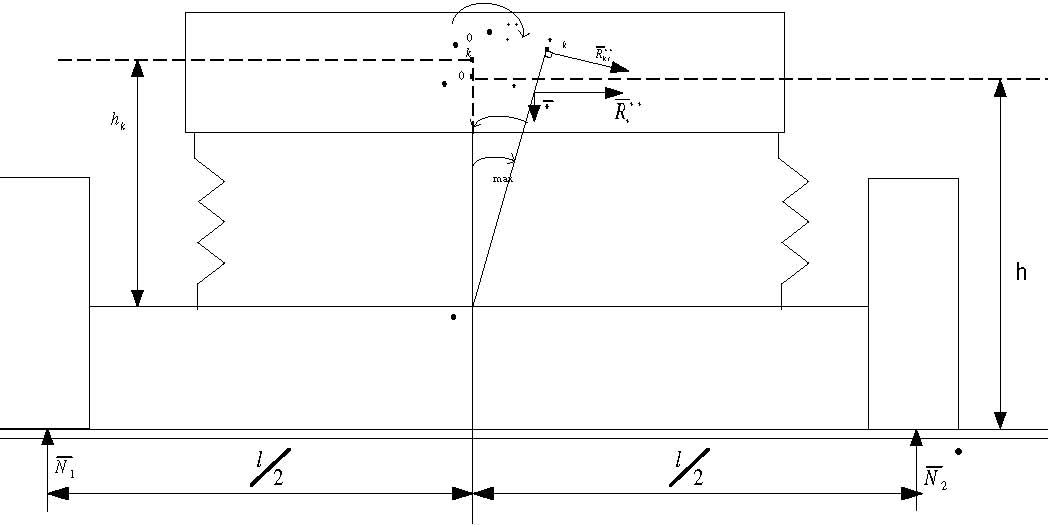
Рис. 8. Расчетная схема сил, действующих на автомобиль, при учете поперечных колебаний кузова и наклоне кузова на максимальный угол.

 

Пренебрегая при этом малыми величинами первого порядка, уравнения кинетостатики можно привести к виду:

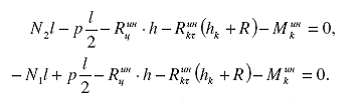 (43)

Решая систему двух линейных алгебраических уравнений (43), найдем:

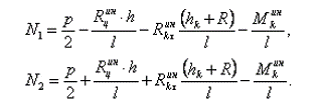 (44)

На основании соотношений (44) с учетом (1), (42), (21) и принятого допущения о симметрии передней и задней осей колес, а также упругих элементов по отношению к центру масс автомобиля нетрудно найти реакции дорожного полотна, действующие на каждое левое и правое колеса.

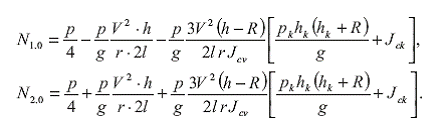 (45)

На основании теоремы Гюйгенса-Штейнера о моментах инерции системы относительно параллельных осей имеем

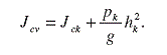 (46)

Учитывая (46) выражения (45) можно преобразовать к виду:

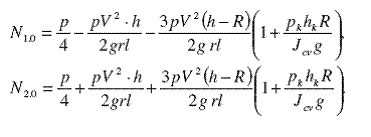(47)

Целесообразно выразить момент инерции кузова J_cv через радиус инерции ρ_cv относительно продольной оси, проходящей через центр крена (точку С_v), а именно

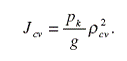 (48)

С учетом (48) соотношения (47) примут вид:

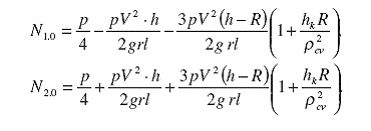 (49)

На основании первого соотношения (49) можно определить критическую скорость, при которой возможно опрокидывание автомобиля.

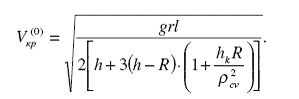 (50)

Выражение для критической скорости автомобиля (50) получено для случая, когда автомобиль оказывается в точке перегиба траектории (т. А ₁), и при этом время движения автомобиля по участку траектории А ₁А ₂ (t) равно половине периода поперечных колебаний кузова

 (то есть τ= ).

Целесообразно исследовать также случай, при котором , то есть когда максимальный угол наклона кузова при движении автомобиля по участку траектории А ₁А ₂ будет в момент t<τ , определяемый по (28). При этом поперечные колебания кузова описывается уравнением (23) и, следовательно

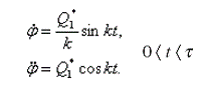 (51)

Определим  и  в момент, когда угол наклона кузова будет максимальным, то есть в момент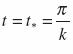

 (52)

На основании (37) – (39) и (52) получим

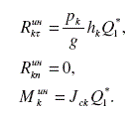 (53)

Система уравнений (43) с учетом соотношений (1), (53), (21) и принятой расчетной модели автомобиля позволяют определить реакции дорожного полотна на каждое левое и правое колеса.

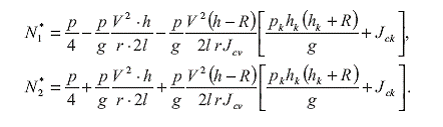 (54)

Соотношения (46) и (48) позволяют преобразовывать (54) к следующему виду:

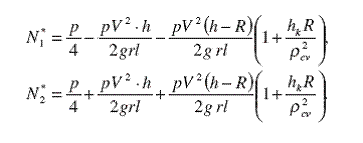 (55)

Как было указано ранее начало опрокидывания автомобиля возможно при равенстве нулю реакции, действующей на менее нагруженные колеса, то есть

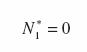 (56)

В результате подстановки (55) в (56) определим величину критической скорости, при которой может произойти опрокидывание автомобиля во время его движения по участку траектории А ₁А ₂.

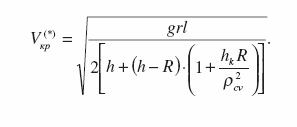 (57)

Сравнивая критические скорости автомобиля, найденные при учете только центробежной силы инерции автомобиля (4) с критическими скоростями, найденными и при учете, кроме того, поперечных колебаний кузова (50) и (57), можно сделать следующие выводы:

1. Поперечные колебания кузова могут оказать существенное влияние на величину критической скорости автомобиля (в сторону ее уменьшения), при которой возможно его опрокидывание.

Это, прежде всего, относиться к случаям, когда радиусы кривизны траектории при объезде препятствия меняются скачками, то есть центробежные силы инерции возникают и исчезают внезапно и также внезапно возникают центробежные силы инерции противоположного направления.

2. Наименьшая критическая скорость автомобиля возможна в точке перегиба траектории (в т. А ₂) при условии, что время движения

до этой точки совпало с половиной периода поперечных колебаний кузова ().

3. В случае, когда время движения автомобиля до точки перегиба траектории больше половины периода колебаний кузова ( ), критическая скорость, найденная в момент t_* равный половине периода колебаний кузова (), 1. будет заметно меньше критической скорости, полученной при учете только центробежной силы инерции, но больше критической скорости, соответствующей случаю

2. Получена принципиальная возможность создания компьютерной модели более точного анализа влияния различных динамических и конструктивных параметров автомобиля на его устойчивость при объезде препятствия, а также определения при этом оптимальных соотношений конструктивных и эксплуатационных параметров различных типов автомобиля.

 

Литература:

1.        Иларионов В.А. Поперечный крен кузова и устойчивость автомобиля, «Автомобильная промышленность», 1962, IV10, С 29-32.

2.        Ретенберг Р.В. Подвеска автомобиля, М.: Машиностроение, 1972, 392с.

3.        Добронравов В.В. Никитин Н.Н., Курс теоретической механики, М.: «Высшая школа», 1983, 575с.

4.        Тимошенко С.П., Янг Д.Х. Уивер У. Колебания в инженерном деле. М.: «Машиностроение», 1985, 472с.