Муравьёва Л.Г., старший преподаватель кафедры менеджмента филиала Тихоокеанского государственного экономического университета в г. Южно-Сахалинске

Статья посвящена исследованию специфики франчайзинга как формы предпринимательской деятельности, показана необходимость определения выгодности сделки для крупной и малой фирм с учетом различных факторов. На основе представленной в математической литературе теории игр разработана модель, позволяющая определить какую выгоду получат участники сделки с учетом первоначального капитала, различных взносов малого предприятия, роялти, риска, бренда крупной фирмы.

 

Ключевые слова: крупный бизнес, франчайзинг, теория игр.

 

THE MODEL OF OPTIMUM INTERACTION OF LARGE BUSINESS WITH SMALL ENTERPRISES

Muravyova L., the senior teacher of chair of management of branch of Pacific state economic university in Yuzhno-Sakhalinsk

Article is devoted specificity research franchising as forms of enterprise activity, necessity of definition of advantage of the transaction for large and small firms taking into account various factors is shown. On the basis of the theory of games presented in the mathematical literature the model is developed, allowing to define what benefit participants of the transaction taking into account the initial capital, various payments of a small enterprise, a royalty, risk, a large firm brand will receive.

 

Key words: large business, franchising; the theory of games.

 

В случае нехватки ресурсов для самостоятельной организации бизнеса одним из вариантов устойчивого развития малых предприятий является сотрудничество с крупными фирмами в форме франчайзинга.

Целью статьи является разработка модели взаимодействия крупного и малого бизнеса на основе франчайзинга.

Достижение данной цели определяется решением следующих задач:

-         уяснение сущности франчайзинга, как особой формы ведения бизнеса;

-         построение модели взаимовыгодной франчайзинговой сделки;

-         определение размера выгоды для сторон франчайзинга с использованием цифрового материала (апробация модели).

Франчайзинг - это такая форма организации бизнеса, при которой крупная компания передает малому предприятию право на производство и продажу продукта (услуг) этой компании.

Франчайзинговые взаимоотношения могут быть прибыльными для обеих сторон. Так, крупная компания получает выгоды в форме расширения рынков сбыта, укрепления своих конкурентных позиций, получения дополнительного дохода (первоначальная продажа франшизы, продажа специальных услуг, роялти). Малые предприятия получают ощутимую помощь, которая проявляется в возможности начать собственное дело в проверенной рыночной нише, предоставлении технологии производства, обучении персонала, консалтинге, экономии на поставках сырья, материалов, оборудования, возможности продвижения товара под торговой маркой крупной фирмы, экономии на проведении мероприятий по стимулированию сбыта (в т. ч. на рекламе) и др.

В случае принятия решения об использовании франчайзинга как особого способа предпринимательской деятельности руководство малых фирм сталкивается с проблемой определения выгодности франчайзинговой сделки. Поэтому необходимо разработать модель, позволяющую выявить возможности максимизации прибыли с учетом первоначального взноса франшизополучателя (малой фирмы), роялти, бренда владельца франшизы и др. факторов.

Пусть владелец товарного знака (франшизодатель) – “owner” будет идентифицироваться индексом 0, так как данный индекс соотносится с первой буквой английского названия исследуемого объекта. Франшизополучателям присваиваются последовательные индексы, начиная с первого. Стандартными являются символы

p_j – средняя цена товара на предприятии с индексом “j”

q_j – количество выпускаемого товара на предприятии с индексом “j”

c_j – общие издержки на предприятии с индексом “j”

Так как прибыль не имеет общепризнанного обозначения, то мы будем записывать ее по первым двум буквам английского эквивалента (profit)

Следует различать представленные величины до заключения договора франчайзинга и после заключения данного договора. В последнем случае используется значок “шляпки” над соответствующими переменными. Кроме того, заглавные буквы P,Q,C,Pr применяются для экономических показателей коалиции, созданной в результате заключения договора франчайзинга.

Представим обозначения, относящиеся непосредственно к ведению франчайзинга. Пользователь данной формы бизнеса платит вступительный взнос и роялти. Согласно иностранным данным, вступительный взнос может достигать от пяти тысяч до миллиона долларов в зависимости от типа заключаемого договора, а роялти составляет фиксированный процент от общего дохода франшизополучателя – по зарубежным оценкам – около 10% [2].

Соответственно, в математическую модель коммерческого взаимодействия вводятся еще два параметра

Fee – полная величина вступительного взноса фирмы - пользователя

Roy – роялти

Представленные обозначения относились к предприятию – пользователю.

Однако и компания - флагман, предоставляющая франшизу для пользователя определяется двумя важными для заключаемого коммерческого соглашения величинами. Напомним кратко их сущность. Во-первых, основой франчайзинга является широко известное или даже лидирующее положение головной фирмы на рынке. В таком случае у потребителя складывается положительный образ, связанный с торговым знаком лидирующей фирмы. Именно эту положительную часть психологической составляющей в имидже франшизодателя мы будем называть брендом. Так как психологические термины с трудом трансформируются к математическим понятиям, то мы выразим бренд в виде процента, а точнее в десятичном числе, лежащим на интервале [0,1], которое получается после приведения процентов к вещественным переменным. Итак

Br – бренд, десятичное число, принадлежащее отрезку [0,1]

Заключение договора несет для лидирующего в своей области деятельности предприятия определенные риски. Не смотря на многочисленные проверки, пользователи франчайзинга часто нарушают условия договора и снижают качество продукции, первоначально определяемое фирмой-владельцем. В результате положение головного предприятия на рынке может быть подорвано и существует определенный риск снижения деловой репутации, а значит и уменьшения доходов. Чтобы учесть данную составляющую мы введем значение риска, также как и бренд, выраженного в процентах или эквивалентных десятичных числах.

R – риск от снижения деловой репутации предприятия франшизодателя в результате невыполнения основных условий договора пользователями. Риск принадлежит отрезку [0,1].

Разумеется, ни бренд, ни риск не могут достигать 100%, то есть доходить до правой точки интервала, однако быстрое убывание при приближении к данной границе будут учитываться соответствующими функциями. Мы также введем функцию потерь (Losses), переводящую вероятностное представление риска в денежное выражение.

В общем случае

L(R) – функция потерь, представляющая зависимость товарооборота головной фирмы от величины риска.

Дальнейшее изложение представляет собой видоизмененную задачу торга, широко известную в математической экономике после появления в 1950 году статьи Джона Нэша “Проблема торгов” (The Bargaining Problem). Не смотря на почтенный возраст приведенной публикации, по признанию ведущих специалистов решение Нэша остается одним из самых эффективных способов решения данной проблемы.

Перейдем к сущности задачи, применительно к запросам франчайзинга.

Рассматривается игровая система с двумя участниками. Вводится пространство состояний на двумерной координатной плоскости. Согласно Нэшу эта область называется пространством полезностей – X = (x₁,x₂) [1]. В нашем варианте полезности имеют конкретное экономическое выражение в виде прибылей, получаемых каждым из участников от введения франчайзинга. Ниже мы приведем выражения прибылей через факторы, рассмотренные выше. В пространстве полезностей указывается точка разногласия (disagreement point) или статус кво [1]. Она указывает, какую полезность получат игроки, если не смогут договориться. Применительно к франчайзингу d₁, d₂ – прибыли, получаемые владельцем и получателем договора до его заключения.

Рассмотрим поведение решения на пространстве полезностей в общем случае, без формирования конкретных вариантов.

Во-первых, полезности естественно должны удовлетворять условию индивидуальной рациональности [1]. Данное условие гласит, что от соглашения должны выигрывать оба партнера, то есть

x₁> d₁; x₂> d₂;

Отметим, что если для франшизодателя данное положение всегда выполняется, хотя бы потому, что пользователь платит вступительный взнос независимо от получаемой прибыли, то для пользователя заключение договора представляет собой больший риск, особенно, если схемы договора применительно к данному региону выполняются впервые и нет опыта их эффективного приложения.

Во-вторых, решение должно быть Парето эффективной точкой в Х [1]. Оптимум по Парето гласит, что благосостояние коалиции достигает максимума, а распределение ресурсов становится оптимальным, если любое изменение этого распределения ухудшает благосостояние хотя бы одного субъекта экономической системы. В ситуации, оптимальной по Парето, нельзя улучшить положение любого участника экономического процесса, одновременно не снижая благосостояния как минимум одного из остальных. Такое состояние рынка называется Парето-оптимальным состоянием. Согласно критерию Парето (критерию роста коллективного благосостояния), движение в сторону оптимума возможно лишь при таком распределении ресурсов, которое увеличивает благосостояние по крайней мере одного участника процесса или договора, не нанося ущерба никому другому.

В литературе [1] рассматривается два подхода к решению представленной задачи с помощью различного поведения лиц, участвующих в договоре франчайзинга. В первом случае каждый участник требует, чтобы договор оказался равновыгодным. Для этого варианта приращения полезностей по сравнению с исходной точкой d должны оказаться одинаковыми. Математически последнее условие приводит к равенству:

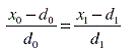
Решение, удовлетворяющее соответствующему тождеству называется “эгалитарным” (от француского egalitaire – “уравнительный”) [1]. Иногда требуют, чтобы в данное тождество входили не отношения, а абсолютные приросты:

но понятно, что игроки разного веса “не могут потреблять одинаковое количество ресурсов”.

Во втором варианте коалиции преимущественным становится максимизация общего успеха

Применительно к франчайзингу, сохраняющему финансовую самостоятельность каждой из сторон вариант достижения максимума общей прибыли вряд ли интересен каждой из сторон. Напомним, что последний вариант относится к утилитарному поведению, при котором каждый участник утверждает “Вы должны сделать нечто, потому что это принесет мне больше пользы, чем Вам вреда”.

Сформулируем авторскую точку зрения на постановку задачи.

Функция Нэша

 (1.1)

при условии, что

 (1.2)

В дальнейшем мы выразим игровые переменные

(x₀, x₁, d₀, d₁) через параметры франчайзинга, однако в настоящий момент необходимо прокомментировать экономическую сущность условий (1.1) и (1.2). Функция Нэша позволяет одновременно учесть выгодность игры для обоих игроков в самой простой формуле произведения. Можно придумать бесконечное множество соотношений, аналогичных функции Нэша, однако все они требуют определенного обоснования, которое трудно провести из-за трудности перевода практической экономики на математический язык. Поэтому, наряду с производственной функцией Кобба – Дугласа произведение Нэша является одним из самых простых и эффективных экономико-математических инструментов.

Условие (1.2) означает, что общий доход двух участников не может превышать определенной величины. Определенное значение данной величины формируется только в процессе практики, однако понятно, что в реальных условиях доход не бывает беспредельным. Верхнюю планку дохода устанавливает постоянная MaxIncome. Здесь необходимо сделать следующее замечание, аналог которого приведен в работе [1]. В неравенстве (1.2) подразумевается, что доходы участников от игры учитываются в одинаковой

степени. Однако можно придать весовые функции λ=(λ₁, λ₂)соответствующим результатам и тогда вместо разностей x₀ − d₀ и x₁ − d₁ в действия вступят нормированные аналоги

λ₀(x₀ − d₀) и λ₁(x₁ − d₁) . На произведение Нэша весовые коэффициенты воздействовать не будут, так как их применение не изменит точки максимума, а повлияет только на его величину. Однако линейное ограничение станет выглядеть следующим образом:

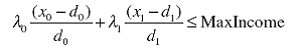
Но мы не будем придавать участникам игры различные весовые категории, опять же из-за трудности их учета в реальных условиях.

Условия (1.1) и (1.2) приводят к задаче нелинейного программирования. Графически решение данной задачи представлено на рис 1. Для удобства визуализации выбраны координаты (x₁,x₂), привязанные к точке разногласия, то есть сдвинутые на (d₁,d₂). На рисунке показаны кривые безразличия функции Нэша

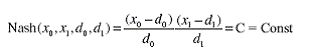
для различных значений постоянной “C”. На экономическом языке – это кривые безразличия для выигрыша обоих игроков. Вдоль этих линий при любой комбинации (x₁,x₂), в обобщенном смысле Нэша коалиция игроков имеет одинаковый выигрыш. С другой стороны на коалицию действуют “силы природы ”- “невидимая рука рынка”, противодействующая игрокам получению неограниченного успеха. Она приводит к тому, что создается допустимое множество игровых ситуаций, ограниченное прямой и координатными осями.

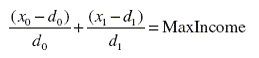
Понять решения игры – то есть получение максимального результата, можно легко, если привлечь к рассмотрению рис. 1. С ростом выигрыша коалиции линии уровня функции Нэша сдвигаются к правому верхнему углу. Первоначально, так как это действует для кривой Nesh = C₁, они находятся внутри допустимой области, однако игроков не удовлетворяет малая величина выигрыша. Например, положение Nesh = C₃ их бы устроило в большей степени, однако при такой ситуации кривая безразличия функции Нэша выходит за пределы допустимой области и игра не имеет решения. Поэтому, оптимальным будет вариант, при котором выпуклая линия безразличия продвинулась как можно далее в сторону увеличения постоянной “C”, однако сама линия еще находится внутри допустимой области. Естественное решение при таком подходе – поиск максимума, как точки касания. На рисунке найденная подобным образом точка обозначена через Max.

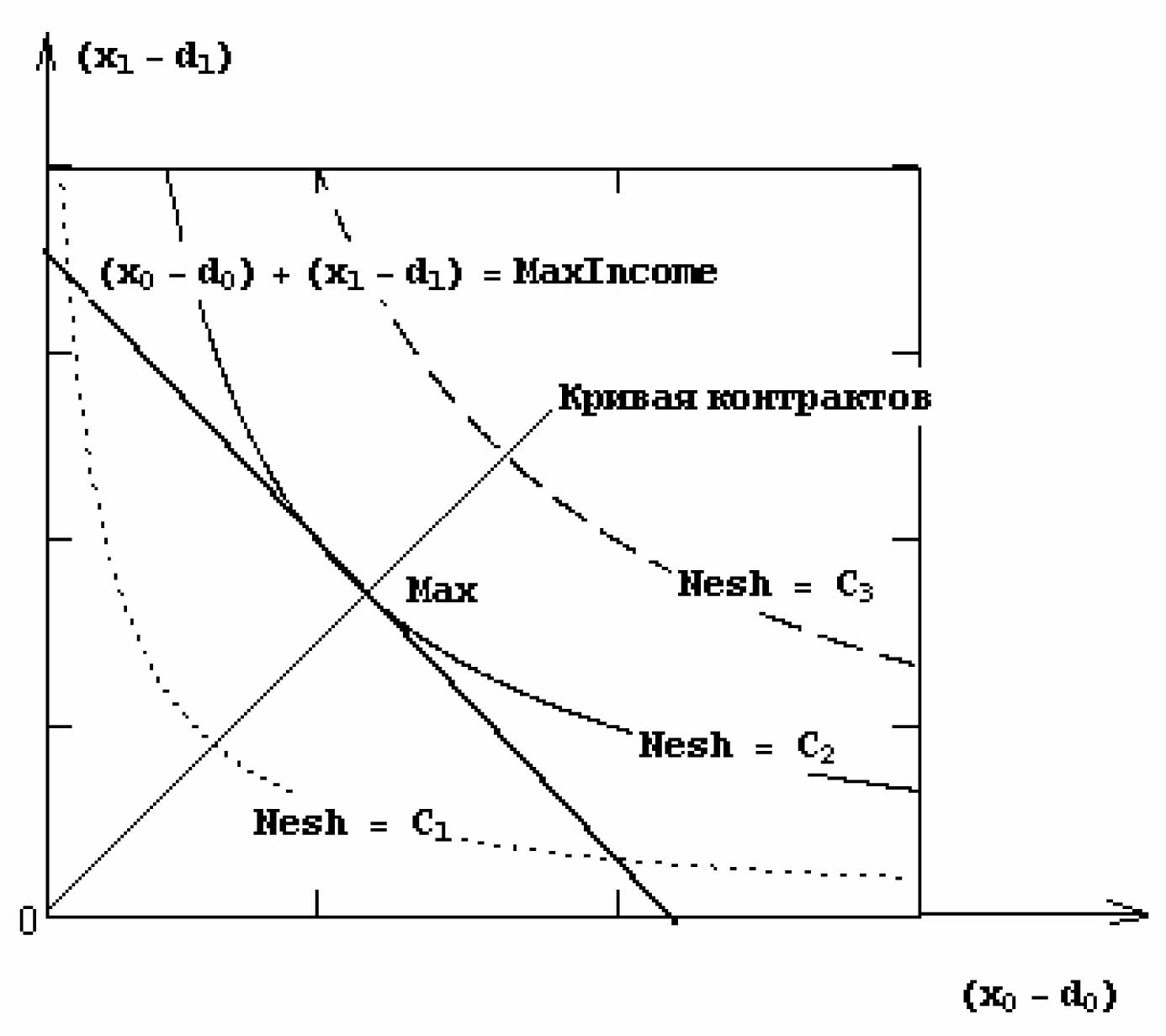
Рис. 1 Оптимизация игры по Нэшу

 

Мы предполагаем, что распределение благ происходит не между двумя участниками игры – то есть договаривающимися сторонами франчайзинга, а между участниками этого договора и внешним миром. Как уже говорилось ранее, рынок препятствует достижению неограниченных результатов для членов коалиции и принуждает выбирать в результате некоторых действий, которые в теории называются “переговорами с природой” [1], некоторые оптимальные пути развития. В связи с тем, что “бюджетная кривая”

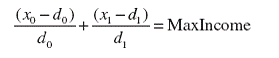
меняет свое положение в зависимости от постоянной MaxIncome – то есть в зависимости от ресурсов отпущенных “природой” участникам игры оптимальный путь развития проходит через все возможные точки касания. Если кривые безразличия касаются друг друга в данной точке, то любое другое распределение ресурсов будет хуже хотя бы для одного из участников, т.е. в этом случае не существует взаимовыгодного обмена. Эти точки называются в научной литературе [1] - эффективными по Парето, а множество всех таких точек представляет собой “кривую контракта” или “переговорную кривую”. Если начальное распределение ресурсов неэффективно (то есть соответствующая точка не лежит на кривой контракта), то добровольный обмен благами будет проводиться до тех пор, пока полученное распределение не станет Парето-эффективным. Эта точка, от которой невыгодно отклоняться ни одному из субъектов, называется равновесием при заключении контрактов между внешним миром и участниками игры. Множество равновесий образует ядро игры и является подмножеством контрактной кривой.

Ядро – это множество допустимых распределений ресурсов в экономике, которые не могут быть улучшены никаким множеством агентов (коалицией). Понятие ядра аналогично равновесию Нэша в некооперативных играх: исход является устойчивым, если никому из игроков не выгодно от него отклоняться. Говорят, что коалиция может блокировать некоторое допустимое распределение благ, если ее члены получают большую полезность при другом допустимом распределении, которое отличается от данного только тем, что часть членов данной коалиции потребляет другие наборы товаров, которые в сумме не превышают имеющегося набора общедоступных благ и начальных запасов членов коалиции. Ядром называется множество допустимых распределений благ, таких, что не существует у коалиции – в нашем варианте – “внешних условий”, которая может их блокировать. Другими словами, как бы ни старались явные или неявные контрагенты франчайзинга нарушить оптимальное решение, которое образует ядро (в нашем варианте – “кривая контракта”) они не смогут.

Определим теперь точным образом значения переменных, при котором наступает точка максимума. Для удобства введем сдвинутые переменные

z₀ =x₀ −d₀ ; z₁ =x₁ −d₁ ;

Тогда на линии уровня функция Нэша имеет вид

Z₁z₀ =C

а допустимая область выражается условиями:

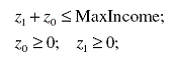
В точке касания должны равняться между собой значения функций и значения их первых производных, так как угловые коэффициенты касающихся функций должны совпадать. Если считать z₀ за независимую переменную, то

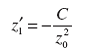
Таков угловой коэффициент выпуклой кривой безразличия. Бюджетная прямая имеет угловой коэффициент (-1). Приравняв, получим:

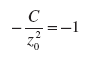
откуда в точке максимума

Выразим постоянную “C” через величину бюджета. Из уравнения прямой

Подставим значения координат в функцию Нэша

и раскроем скобки

В результате

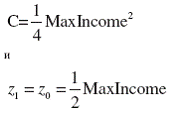
Таким образом, решение задачи Нэша приводит к “эгалитарныму” тождеству

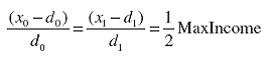 (1.3)

Очевидно, что это тождество означает равный относительный прирост капитала для лиц, вступивших в франчайзинговую сделку.

Вернемся к экономической сущности игровых переменных. Очевидно, что точка разногласия “d”– это первоначально получаемая прибыль.

После заключения договора франчайзинга объем торгов и стоимость продукта головной фирмы практически не меняется, зато добавляется вступительный платеж младшего партнера – Fee и его регулярно выплачиваемые роялти – Roy %. Однако возможно существование потерь Losses (R), которые зависят от риска R “плохого поведения” фирмы, заключившей договор. Итак

 (1.4.1)

Напомним, что шляпки над переменными означают их величины после заключения договора франчайзинга. Для предприятия франшизополучателя

 (1.4.2)

Применяя естественные обозначения для прибыли, получим

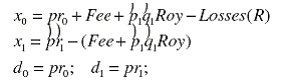
Условие эгалитарности, означает, что

 (1.4.3)

Для удобства введем еще два обозначения

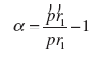- относительный прирост прибыли франшизо

получателя за счет появления фрачайзинга.

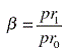- первоначальное отношение прибылей франшизополучателя и франшизодателя.

За счет появления этих переменных равенство (1.4.3) запишется следующим образом:

 (1.5)

Для упрощения данного уравнения будем считать, что риск потерь головной фирмы из-за непредсказуемого поведения франшизополучателя практически равен нулю, то есть Losses( R )=0. Кроме того, отношение

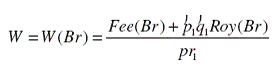 (1.6)

мы будем считать функцией бренда. Тогда относительный прирост прибыли франшизополучателя за счет появления франчайзинга выражается соотношением

 (1.7)

Последнее равенство означает, что прирост прибыли линейно зависит от первоначального отношения прибылей франшизополучателя и франшизодателя І и более сложным способом предопределяется брендом предприятия (рис. 2), предоставляющего франчайзинг.

 

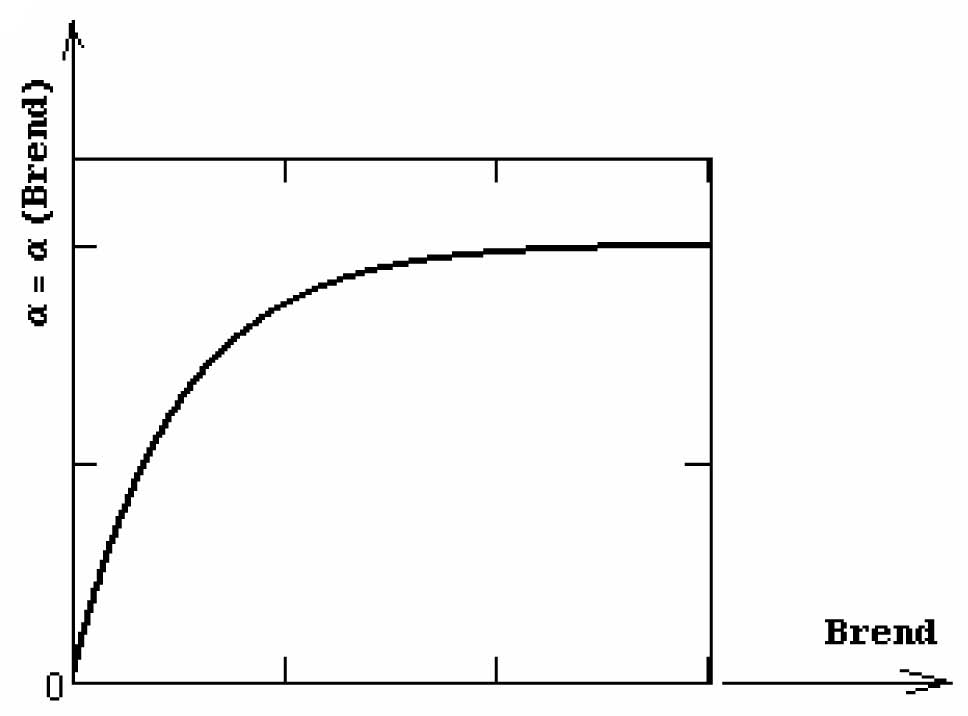
Рис. 2. Отношение получаемой прибыли к первоначальной для франшизополучателя в зависимости от бренда головного предприятия

 

Ясно, что по закону убывающей полезности влияние бренда будет затухать вместе с его увеличением. Кроме того, нулевой бренд, естественно не даст никакой прибыли обеим фирмам.

Данную модель взаимодействия крупной фирмы и малого промышленного предприятия необходимо представить в виде цифрового материала (данные условные).

Построим кривую безразличия функции Нэша (Nesh =C₁), отражающую взаимодействие крупной фирмы и первого малого предприятия. При этом значения прибыли до франчайзинга (d₀ и d₁) постоянны.

Так, при

d₀ = 10 тыс. руб., х₀ = 20 тыс. руб.

d₁= 5 тыс. руб., х₁ = 20 тыс. руб.

 

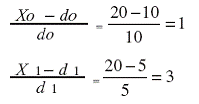
При

х₀ = 25 тыс. руб., х₁ = 15 тыс. руб.

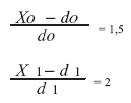
При х₀ = 30 тыс. руб., х₁ = 10 тыс. руб.

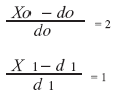
При х₀ = 33 тыс. руб., х₁ = 8 тыс. руб.

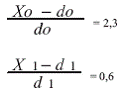
Нанесем полученные значения на график (рис. 3). Очевидно, при увеличении прибыли собственника (х₀ - d₀) выгода малой фирмы от франчайзинга снижается (х₁ – d₁).

 

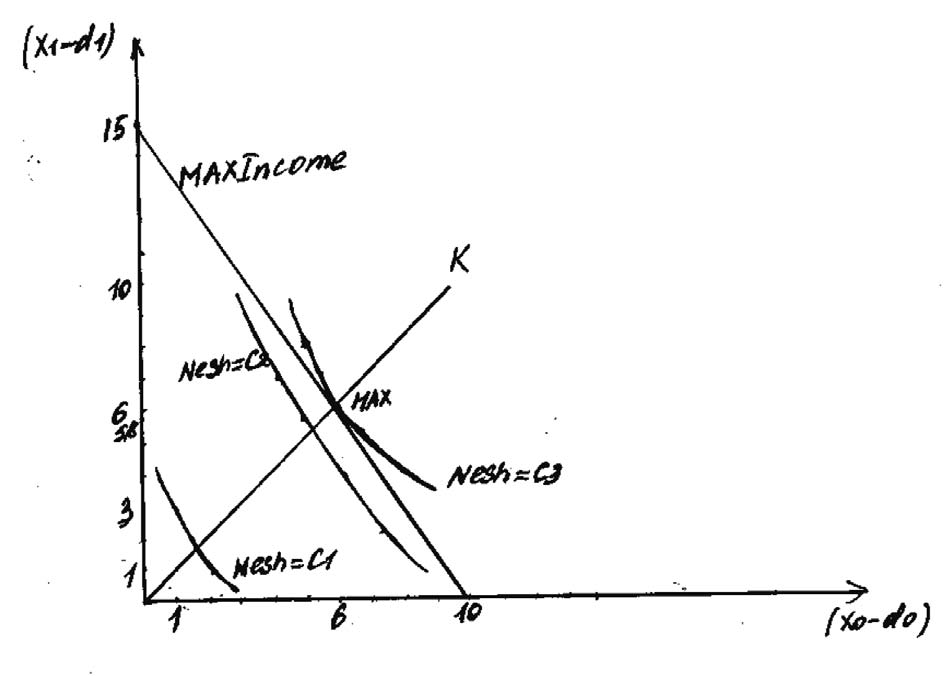
Рис. 3. Оптимизация игры для фирм, работающих по франчайзингу

 

Верхнюю планку прибыли устанавливает постоянная MaxIncome, которая определяется как (х₀ - d₀) + (х₁ – d₁).

В нашем случае:

(х₀ - d₀) = 20 – 10 =10

(х₁ – d ₁) =20 – 5 =15

MaxIncome = 10 +15 =25

Таким образом, максимальный прирост прибыли крупной и малой фирм составляет 25 тыс. руб.

Построим кривую безразличия функции Нэша (Nesh =C₂), отражающую взаимодействие крупной фирмы и второго малого предприятия.

При этом значения прибыли до франчайзинга (d ₀ и d₁) также постоянны.

Так, при

d₀ = 10 тыс. руб., х₀ = 50 тыс. руб.

d₁= 5 тыс. руб., х₁ = 40 тыс. руб.

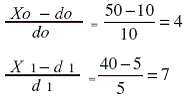
При х₀ = 60 тыс. руб., х₁ = 35 тыс. руб.

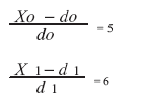
При х₀ = 80 тыс. руб., х₁ = 15 тыс. руб.

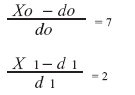
Очевидно, с ростом прибыли крупной и малой фирм линии уровня функции Нэша сдвигаются к правому верхнему углу. Однако кривая Nesh = C₂ находится внутри допустимой области, что свидетельствует о низкой степени удовлетворенности игроков величиной выигрыша (прибыли).

Построим кривую безразличия функции Нэша (Nesh =C₃), отражающую взаимодействие крупной фирмы и третьего малого предприятия. При этом значения прибыли до франчайзинга (d₀ и d₁) также постоянны.

Так, при

d₀ = 10 тыс. руб., х₀ = 60 тыс. руб.

d₁= 5 тыс. руб., х₁ = 45 тыс. руб.

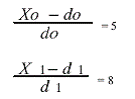
При х₀ = 65 тыс. руб., х₁ = 40 тыс. руб.

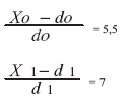
При х₀ = 70 тыс. руб., х₁ = 34 тыс. руб.

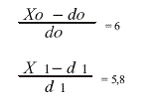
При х₀ = 80 тыс. руб., х₁ = 30 тыс. руб.

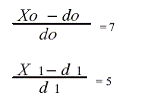
При х₀ = 90 тыс. руб., х₁ = 25 тыс. руб.

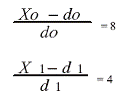
На рис. 3. видно, что выпуклая линия безразличия Nesh =C₃ продвинулась в сторону увеличения постоянной “C”, однако сама линия еще находится внутри допустимой области – это оптимальный вариант взаимодействия крупного и малого промышленных предприятий. Естественное решение при таком подходе – поиск точки касания (максимума). На рисунке найденная подобным образом точка обозначена через Max. Точка Мах свидетельствует об эффективном распределении ресурсов, что приводит к взаимовыгодному обмену. Кривая (К), соединяющая кривые безразличия, называется «кривой контракта», от точки пересечения которых участникам сделки отклоняться невыгодно.

Для того, чтобы определить значение точки максимума, необходимо отметить, что в данной точке должны равняться между собой значения функций.

Согласно формулы (1.3):

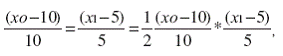
 То есть

х₀ = 69 тыс. руб.

х₁ = 34,5 тыс. руб.

Таким образом, при получении крупной фирмой прибыли в размере 69 тыс. руб., а малой фирмой 34,5 тыс. руб. будет наблюдаться равный относительный прирост капитала для лиц, вступивших во франчайзинговую сделку. При формировании прибыли необходимо учитывать первоначальный взнос малого предприятия в размере 15 тыс. руб. (данные условные) и регулярно выплачиваемые роялти – 10 % от дохода. В этом случае прибыль владельца франшизы составляет (по формуле 1.4.1):

х₀ = 10 + 15 + 50*0,1 -Losses( R )

х₁ = 30 тыс. руб. - Losses( R )

А прибыль франшизополучателя составляет (по формуле 1.4.2):

х₁ =35 –(15 +50*0,1)

х₁ = 15 тыс. руб. Предполагая, что риск потерь головной фирмы из-за непредсказуемого поведения франшизополучателя практически равен нулю, то есть Losses( R )=0, получаем равенство (формула 1.4.3):

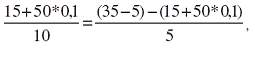
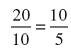, следовательно, 2=2

Данное равенство показывает взаимовыгодное сотрудничество крупного и малого предприятий с учетом различных составляющих франчайзинговой сделки.

Исходя из функции бренда (1.6) можно рассчитать относительный прирост прибыли франшизополучателя после заключения договора франчайзинга.

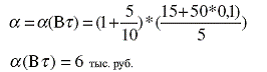
Таким образом, прирост прибыли линейно зависит от первоначального отношения прибылей франшизополучателя и франшизодателя и более сложным способом предопределяется брендом предприятия, предоставляющего франчайзинг.

Разработанная модель франчайзинга позволяет предвидеть возможную выгоду (потери) от заключения сделки с учетом ранее получаемой прибыли, первоначального взноса, роялти, риска и бренда владельца франшизы.

Очевиден факт, что взаимодействие малого и крупного бизнеса является одним из основных факторов повышения конкурентоспособности действующих предприятий.

 

Литература:

1.        Данилов В.И. Лекции по теории игр. М.: Российская экономическая школа, 2002.

2.        Franchise Business Economic Outlook, prepared by “The International Franchise Association Educational Foundation”, January 7, 2009, 22 p