Туфетулов А., соискатель КГУ

Реализация программы отраслевой реструктуризации на уровне региона возможна лишь в том случае, если все хозяйствующие субъекты региона подчинены общей региональной стратегии развития. В этом случае все они могут быть организационно консолидированы и их усилия могут быть сконцентрированы на решении задач отраслевой реструктуризации.

 

FINANCIAL RESOURCES OF BRANCH RE-STRUCTURING OF REGIONAL ECONOMY

 

Tufetulov A., Competitioner of KSU

Realisation of the program of branch re-structuring at region level is possible only in the event that all managing subjects of region are subordinated the general regional strategy of development. In this case all of them can be organizational consolidated and their efforts can be concentrated on the decision of problems of branch re-structuring.

 

Ключевые слова: финансовые ресурсы, реструктуризация, регион, модель Марковица

 

В настоящее время при наличии в регионе нескольких наиболее важных продуктов возникает задача управления региональной экономикой как портфелем бизнесов или бизнес-портфелем. В этой ситуации, как правило, возникает большое количество неопределенных ситуаций, которые необходимо учитывать при принятии стратегических решений. В настоящее время существует достаточно инструментов учета этих неопределенных ситуаций. Одним из них являются нечеткие множества.

Рассмотрим ситуацию, когда руководство региона, как координатор и руководитель региональной экономики управляет ей, руководствуясь определенными стратегическими и тактическими соображениями и приоритетами отраслевой реструктуризации. Одним из главных критериев выбора приоритетного направления отраслевой реструктуризации является совокупный доход регионального бюджета. В классической ситуации доход регионального бюджета зависит от количества налогоплательщиков и среднего объема налоговоых платежей.

С учетом российской специфики региональное руководство стремится создать несколько крупных налогоплательщиков, чтобы они формировали практически всю налогооблагаемую базу. Помимо критерия дохода не менее важным является критерий финансовой устойчивости региональной экономики, который определяет риски регионального бюджета в связи с банкротством налогоплательщиков. Превышение удельного веса банкротов в общем количестве налогоплательщиков является основой для принятия решения об отраслевой реструктуризации.

В настоящее время методик для определения уровня эффективности региональной экономики практически не существует. Наиболее приемлемым является показатель взвешенной по доле отчислений в бюджет отраслевой эффективности, суть которого в расчете бюджетного эффекта региональной экономики, сопоставленного, например, с валовым региональным продуктом. На основании взвешивания у регионального руководства появляется возможность измерить эталонное значение эффективности региональной экономики (Э_РЭ) по следующей формуле:

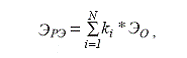
где

N – количество отраслей, присутствующих в экономике региона;

k – удельный вес платежей отрасли в общем объеме налоговоых платежей в региональный бюджет;

Э_о – среднеотраслевая эффективность хозяйствующих субъектов в масштабах всей отрасли национальной экономики.

На основании указанной формулы рассчитывается эталонное значение эффективности региональной экономики. Если фактическое значение ниже эталонного, значит проблема реструктуризации должна решаться незамедлительно, если фактическое значение выше эталонного, значит отраслевая структура региональной экономики удовлетворительная. Таким образом, региональная экономика представляет собой портфель отраслей, для которого могут использоваться различные портфельные стратегии на основании описанного выше критерия реструктуризации. В связи с изложенным, мы считаем уместным описать различные варианты портфельного управления применительно к экономике региона.

Как известно, классической моделью портфельного управления является модель Марковица¹. Сущность данной модели широко известна, однако в процессе отраслевой реструктуризации региональной экономики данная модель рассматривается нами впервые. Пусть региональный экономический портфель содержит N стратегических отраслей по видам продукции, каждая из которых характеризуется пятью параметрами²:

• • средней добавленной стоимостью отрасли в базовом периоде AV_i0;
• числом хозяйствующих субъектов n_i в каждой отрасли;
• валовым отраслевым продуктом ВОП_i0 хозяйствующих субъектов региона в начальный период времени.

Тогда: ВОП _i0 = AV _i0 * n _i.

Валовый отраслевой продукт является случайной величиной и может иметь нормальное распределение с параметрами:

(AV _i0 * (1 + r _i), s _i),

где

• r _i – ожидаемая эффективность отрасли;
• s_i – стандартное отклонение отраслевой эффективности от средневзвешенной эффективности региональной экономики.

При этом сам портфель характеризуется:

• • валовым региональным продуктом в момент времени t – ВРП_t;
• корреляционной матрицей {r_ij}, коэффициенты которой характеризуют связь между эффективностями i-й и j-й отрасли;
• долевым стоимостным распределением отраслей в региональном портфеле {x_i}, причем для исходного портфеля выполняются следующие условия:

         для начального периода³:

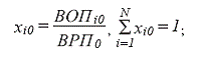
         для текущего периода:

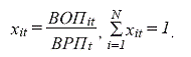
Значение коэффициента r_ij определяется по формуле коэффициента парной корреляции⁴:

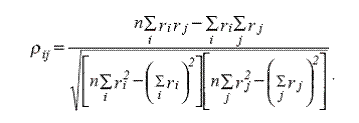
Таким образом, портфель описан системой статистически связанных случайных величин с нормальными законами распределения. Тогда, согласно теории случайных величин, ожидаемая эффективность региональной экономики, рассматриваемой как портфель отраслей, в определенный момент времени r находится по формуле: t

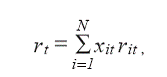(1)

а стандартное отклонение портфеля (разброс эффективностей от регионального значения) s, характеризующее степень риска региональной экономики, определяется по формуле:

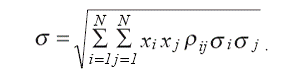(2)

Задача управления таким портфелем имеет следующее описание: определить вектор {x_it}, максимизирующий целевую функцию r_t вида (1) при заданном ограничении на уровень риска s, оцениваемый по формуле (2):

(3)

Но при этом необходимо отметить, что в подходе Марковица к портфельному выбору под риском понимается не риск неэффективности инвестиций, а степень колебаний ожидаемого дохода по портфелю, причем как в меньшую, так и в большую сторону. Можно без труда перейти от задачи вида (3) к задаче, где в качестве ограничения вместо фиксированного стандартного отклонения выступает вероятность того, что эффективность региональной экономики окажется ниже эталонного уровня. На основании анализа различных экспертных мнений, было установлено, что подход Марковица, получивший широчайшее распространение в практике управления портфелями, тем не менее, имеет ряд модельных допущений, плохо согласующихся с реальностью описываемого объекта – региональной экономики. В частности, по мнению экспертов⁵, существуют, как минимум две проблемы:

1. Слабость гипотезы о статистичности случайных процессов. Классическая теория вероятности констатирует статистичность случайных событий в тех условиях, где имеет место статистическая однородность выборки событий. В противном случае практически нецелесообразно использовать строгую статистическую зависимость. Например, если оценивается стоимость жилья в конкретном районе, то на цену влияют не только факторы описывающие сам объект оценки, но и факторы внешней среды, например, тенденции рынка недвижимости. Такая же ситуация складывается и на уровне региональной экономики.

В России регион, наблюдаемый 10 лет назад, и тот же регион сегодня – это, вообще говоря, два различных объекта наблюдения. Изменилось рыночное окружение регионов, их социальный климат, соответственно, изменилась их рыночная позиция: некоторые регионы могли расширить рынок по видам своей продукции (в частности, регионы с преобладанием предприятий топливно-энергетического комплекса и металлургии) или, наоборот, снизить продажи (регионы с преобладанием легкой промышленности и машиностроения).

Соответственно, риск убытков по конкретной отрасли падает или растет, но причина этих колебаний внешняя. Она не имеет прямого отношения к региону, не обусловлена его экономикой. Поэтому нельзя при исследовании экономики конкретного региона говорить о статистической однородности, нельзя говорить о статистичности случайного процесса эффективности отраслей. И, таким образом, нельзя говорить о статистической вероятности того или иного события, связанного со случайной величиной эффекта по конкретной отрасли, при классическом понимании вероятности.

Если же речь идет о совокупности локальных вероятностей, основанных на единичном экспертном мнении, то введение этих вероятностей должно быть предварено специальным обоснованием (исследованием информативности контекста свидетельств об изучаемом объекте, экспертным опросом и т. д.). Когда вероятностная субъективная оценка производится единичным экспертом, риск субъективности и ошибочного прогноза существенно возрастает⁶ . Фактически, применяя субъективные вероятности, эксперт отказывается от частотного понимания вероятности и вкладывает в это понятие собственные субъективные ожидания, которые могут быть существенно искажены оглядкой на предысторию колебаний эффективности конкретной отрасли экономики.

В случае смены рыночных ориентиров эта предыстория перестает быть показательной, объект наблюдения теряет статистическую независимость. Например, в связи с изменением налогового или таможенного законодательства перестает быть актуальной для прогнозов статистика по поступлениям в бюджеты различных уровней, собранная в предшествующие изменению периоды наблюдения.

2. Корреляция как натяжка. Из-за отсутствия статистичности случайных процессов отраслевых доходов, то нет и статистической связи между случайными процессами. Когда коэффициенты корреляции r _ij задаются константами, предполагается, что раз и навсегда известен характер причинно-следственной связи между доходами различных отраслей региональной экономики⁷ .

В рыночных условиях ситуация более сложная, поэтому характер причинно-следственной связи между отраслями не может быть описан одним экспертом рынка с достаточным уровнем точности, а лишь с той или иной степенью приблизительности. Большей достоверности можно добиться, если эксперт вместо чисел употребляет лингвистически нечеткие высказывания с той или иной степенью оттеночной уверенности. К ним относятся высказывания типа: «между отраслями присутствует сильная взаимная зависимость», «динамика отраслей разнонаправлена», «в региональной экономике отрасли связаны относительно», «можно выявить слабую отрицательную связь», «связь, скорее, слабая положительная, нежели нейтральная» и т. п.

В условиях региональной экономики неопределенность носит двумерный характер: с одной стороны, это нечеткость в описании самой ситуации, а с другой стороны – неуверенность эксперта при дифференциации нескольких ситуаций. Лингвистически нечеткое описание связей случайных процессов в условиях существенной информационной неопределенности – это способ для эксперта выражаться предельно четко там, где налицо разительный дефицит четкости. В связи с этим возникает задача формальной интерпретации полученного нечеткого описания в качественный прогноз эффективности региональной экономики.

Указанные замечания к подходу Марковица заставляют региональное руководство вносить коррективы если не в сам подход, то в исходные допущения к модели. Сняв допущение о статистической природе случайных процессов, можно перейти к альтернативному способу учета информационной неопределенности относительно будущего состояния любой отрасли региональной экономики. В этом случае целесообразно применить нечетко-множественный подход. Поскольку отраслевой доход, как и отраслевая эффективность, несмотрия на наличие экономических прогнозов и обоснований во многом случайны, и их точные значения в будущем неизвестны, а вероятностная интерпретация такой случайности не вполне корректна, то в качестве описания эффективности отрасли целесообразно, использовать треугольные нечеткие числа, моделируя экспертное высказывание следующего вида: «Доходность отрасли в конкретном бюджетном периоде ожидаемо равна  и находится в расчетном диапазоне [r₁, r₂]».

В этом случае в экономическом прогнозе происходит отказ от вероятностного описания эффективности, отсекаются наименее вероятные случайные исходы с двух сторон от ожидаемого значе

ния  (вероятность таких исходов при нормальном распределении не равна нулю) и формируется расчетный коридор, в котором находится значение эффективности отрасли. При этом за  принимается либо наиболее ожидаемое, либо среднее значение эффективности в расчетном коридоре.

Функция принадлежности нечеткого числа имеет треугольный вид, если степень субъективной уверенности эксперта в отношении эффективности конкретной отрасли равна нулю за пределами расчетного коридора значений, а максимум этой уверенности, равный единице, достигается в точке . Эксперт убежден, что  заведомо попадет в расчетный коридор эффективности, как бы ни менялись границы этого коридора.

Способ описания ожидаемой эффективности отрасли в форме нечеткого числа может снять проблемы, сопряженные с учетом связи отрасли по тенденциям. Потому что если эффективность конкретной отрасли – треугольное нечеткое число, а эффективность всей региональной экономики – линейная комбинация доходности компонент, то результирующий вид эффективности экономики также известен. Пусть  – эффективность i-й отрасли в форме треугольного нечеткого числа. Тогда эффективность по экономике в целом:

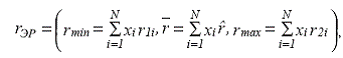 (4)

также является треугольным нечетким числом, где x_i – удельный вес отрасли в региональной экономике. Вывод о том, что линейная комбинация треугольных нечетких чисел есть треугольное нечеткое число – это хорошо известный результат теории нечетких множеств. Пусть r* = const – критическое значение доходности региональной экономики. Если фактическое значение доходности r окажется ниже r*, то считается, что стратегия деятельности и выбора направления отраслевой реструктуризации была разработана с ошибками.

Как известно, уровень убытков по конкретной отрасли можно записать с учетом того, что показатель экономического эффекта отрасли – треугольное нечеткое число. Для целей управления целесообразно зафиксировать – требуемый уровень ожидаемой эффективности региональной экономики. Изменяя значения вектора {x_i}, можно добиться минимального значения риска для регионального бюджета. Получим:

 (8)

Эта задача является двойственной задачей нелинейного программирования. Ее можно трансформировать в следующую задачу:

 (9)

Задача (9) подобна задаче (3), только в качестве фактора риска (линейного ограничения в форме равенства) выступает не стандартное отклонение эффективности отраслей экономики, а уровень убытков по отрасли или неэффективности выбора приоритетных направлений для отраслевой реструктуризации. На основе сформулированных выше основных принципов управления региональной экономической эффективностью на базе нечеткой модели можно проанализировать применение данного подхода на конкретном примере.

Пусть региональная экономика состоит из двух отраслей (О₁ и О₂) со следующими параметрами: эффективность – 16% и 22% соответственно, расчетный коридор О₁ и О₂ – [15,2%, 16,8%] и [21,4%, 22,6%] соответственно. Доля О₁ в региональной экономике (по объему бюджетных платежей) меняется от 0 до 50%, доля О₂ – от 100% до 50% соответственно. Критическое значение эффективности составляет r * = 21,5%. Результаты оценки эффективности и риска по отраслям региональной экономики при перераспределении их долей в портфеле приведены в таблице 1.5.

 

Таблица 1.5 – Определение риска двухотраслевого портфеля с граничной ставкой r*=21,5% годовых

 

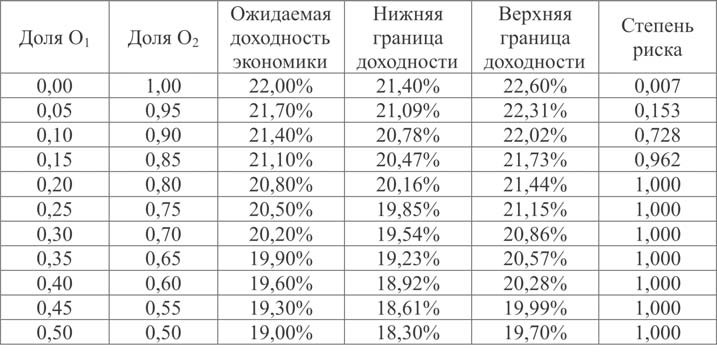
Зависимость «риск – ожидаемая эффективность» по экономике представлена на рисунке 1.2, а зависимость степени риска от доли низкоэффективных отраслей в региональной экономике представлена на рисунке 1.3.

 

 

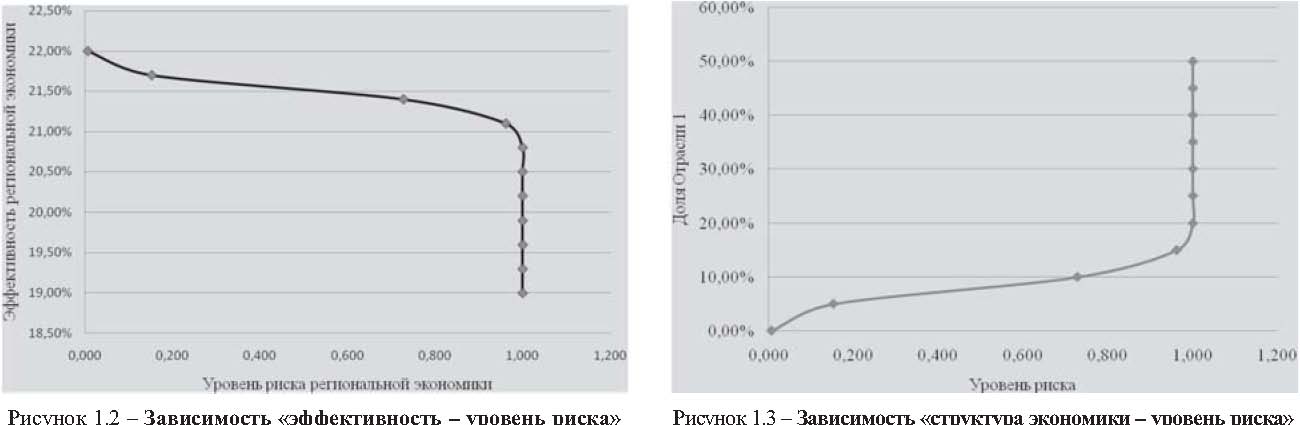
Вполне ясно, что с ростом доли низкоэффективной отрасли в региональной экономике, даже несмотря на то, что расчетный коридор по О₁ более узок, нежели расчетный коридор по О₂, падает ожидаемая бюджетная эффективность экономики в целом – и, соответственно, растет риск убытков и неэффективности бюджета региона. В целях задачи управления риском, если зафиксировать ограничение по ожидаемой эффективности экономики на уровне, например, 21,5%, то минимальный риск такой структуры экономики составит 75%. Этот минимум достигается, когда доля О₁, по данным табл. 1.5, составляет 10%. В альтернативной постановке задачи, когда фиксируется риск, оптимизируется ожидаемая эффективность. Так, при фиксации риска на уровне 40%, максимум эффективности достигается, когда доля О₁ в портфеле составляет 6%.

В рассмотренном выше примере для упрощения ситуации намеренно исключены допущения о надежности бизнеса, то есть фактор риска срыва обслуживания бюджетных обязательств региона. Применение нечетких множеств при учете исходной неопределенности относительно эффектов по отраслям – весьма перспективное направление анализа эффективности региональной экономики при разработке стратегии отраслевой реструктуризации. Руководство региона при использовании этого подхода избавлено от необходимости формировать вероятностные прогнозы на весьма шаткой информационной основе, когда поведение хозяйствующих субъектов в условиях неопределенности рынка не обладает характером статистических случайных процессов. Достаточно сделать допущение о расчетном коридоре, в котором ожидаемо колеблется будущий доход по отрасли. При этих простейших допущениях, как правило, удается оценить степень риска неэффективности выбора отрасли и выполнить мероприятия по минимизации этого риска.

Другим направлением использования теории нечетких множеств при управлении региональной экономикой является определение приоритетных отраслей для развития всей региональной экономики. В данном случае может быть использован дифференцированный подход к отраслевой реструктуризации⁸. Сущность дифференцированного подхода заключается в рассмотрении любой отрасли как самостоятельного объекта управления, являющегося, однако, структурной составляющей региональной экономики.

В этой связи к каждому объекту управления могут быть применены основные принципы дифференцированного управления. В частности, этот подход наиболее эффективен при формировании программы отраслевой реструктуризации, например, при создании региональных хозяйственных комплексов. Критерии важности объекта управления формируются в виде наборов значений соответствующих оценок. Для целей определения приоритетов отраслевой реструктуризации целесообразно рассматривать относительный критерий, позволяющий попарно сравнить отрасли и выбрать приоритетные для повышения их роли в региональной экономике. Рассмотрим алгоритм формирования данного критерия:

1. Все отрасли рассматриваются как самостоятельные экономические объекты bre_j (j = 1,..., J, J – число отраслей региональной экономики).

2. Определяется набор показателей для оценки важности отрасли, который может быть представлен в виде четкого непустого множества D, элементами которого являются свойства важности отрасли d_i (i = 1,..., I, I – число свойств важности).

3. Каждому из элементов d_i присваивается степень важности (вес – p_i). После этого они упорядочиваются в соответствии со степенью важности.

4. Для всех отраслей на множестве свойств важности устанавливаются значения важности v_ij .

5. Для каждой отрасли составляется нечеткое множество D_j:

D_j = {m_ijD(d_i) / d_i},

где

m_ijD(d_i) – функция важности, показывающая, насколько данное свойство важно для данной отрасли региональной экономики:

m_ijD_j (d_i) = p_i * v_ij.

6. Для всех D_j выявляется высота [sup mD(d)], то есть наибольшее из всех полученных значений функции важности: sup mD(d) = m_ijD_j(d_i).

7. Все значения функций важности нормируются: m’_ijD_j(d_i) = m_ijD_j(d_i). sup mD(d).

8. Отрасли реогиональной экономики ранжируются путем сопоставления нормированных функций важности, причем можно говорить, что D_j важнее D_k, если выполняется условие:

N[m’_ijD_j(d_i) > m’_ikD_k(d_i)] > N[m’_ijD_j(d_i) < m’_ikD_k(d_i)],

где N[m’_ijD_j(d_i) > m’_ikD_k(d_i)]  – количество пар функций важности, в которых нормированные значения данных функций множества D_j больше соответствующих значений функций важности множества D_k;

N[m’_ijD_j(d_i) < m’_ikD_k(d_i)] – количество пар функций важности, в которых нормированные значения данных функций множества D_j меньше соответствующих значений функций важности множества D .

Если выполняется обратное условие, то есть:

N[m’_ijD_j(d_i) > m’_ikD_k(d_i)] < N[m’_ijD_j(d_i) < m’_ikD_k(d_i)]

то можно говорить, что D_k важнее D_j. В случае равенства обоих N отрасли одинаково важны для региональной экономики.

Таким образом, можно заключить, что существует механизм нечеткого выбора, в соответствии с которыми может разрабатываться стратегия отраслевой реструктуризации региональной экономики. При этом необходимо отметить, что в рамках региона допустима определенная диверсификация, позволяющая повысить долю отраслевого рынка. В связи с этим, одним из главных конкурентных преимуществ региональной экономики становится умение четко определить стратегические приоритеты и выстроить структуру региональной экономики таким образом, чтобы в ней доминировали наиболее эффективные отрасли, а совокупный риск был минимальным. Для целей минимизации риска в рамках процесса отраслевой реструктуризации должны учитывааться основные угрозы. Рассмотрим эти угрозы подробнее.

 

 

1 Markowitz H. Portfolio Selection: Efficient Diversifications of Investments. New York, Wiley, 1959; Шарп У., Александер Г., Бэйли Дж. Инвести

ции. М.: Инфра-М, 1997; Бригхем Ю., Гапенски Л. Финансовый менеджмент. В 2-х т. Том 1. Санкт-Петербург: Экономическая школа, 1997.

2 Смоляк С. А. Учет специфики инвестиционных проектов при оценке их эффективности // Аудит и финансовый анализ, 1999, №3.

3 Максимов О. Б. Анализ финансового состояния отраслевой корпорации. Основные положения методики. Санкт-Петербург, ИКФ “АЛЬТ”, 1994.

4 Ефимова М. Р., Петрова Е. В., Румянцев В. Н. Общая теория статистики: Учебник. – М.: ИНФРА-М, 1996 – 416 с.

5 Смоляк С.А. Учет специфики инвестиционных проектов при оценке их эффективности // Аудит и финансовый анализ, 1999, №3.

6 Кравец А.С. Природа вероятности. М.: Мысль, 1976.

7 Недосекин А. О. Применение теории нечетких множеств к задачам управления финансами. // Аудит и финансовый анализ. 2000, №2.

8 Бандурин А. В. Управление деятельностью корпораций в России. Дисс. на соиск. уч. ст. д. э. н. – Москва, 2002 г.